Intensity ratio vs. Area ratio: which is the more precise?
A theoretical resolution of a historical problem in analytical chemistry

1. Key Points

• In chemical analysis, the choice between using intensity ratio or area ratio for extracting information from spectra has been the subject of extensive experimental research due to its impact on researchers' decision-making. However, no consistent conclusion has been reached. In this study, we theoretically demonstrate that the area ratio is √2 times more precise than the intensity ratio, thereby resolving this long-standing issue (Figure 1)

• Traditionally, the higher precision of the area ratio over the intensity ratio in experimental results has been attributed to the fact that the area, being an integral of intensity, contains more intensity information. However, our study shows that the superior precision of the area ratio is actually due to the negative covariance between intensity and the full width at half maximum (FWHM).

• By combining analytical solutions that define the limits of spectral parameter measurement with insights from spectroscopy, we have established a theoretical framework linking "analytical precision" with "instrument performance." This framework can guide the most effective equipment upgrades within a limited budget.

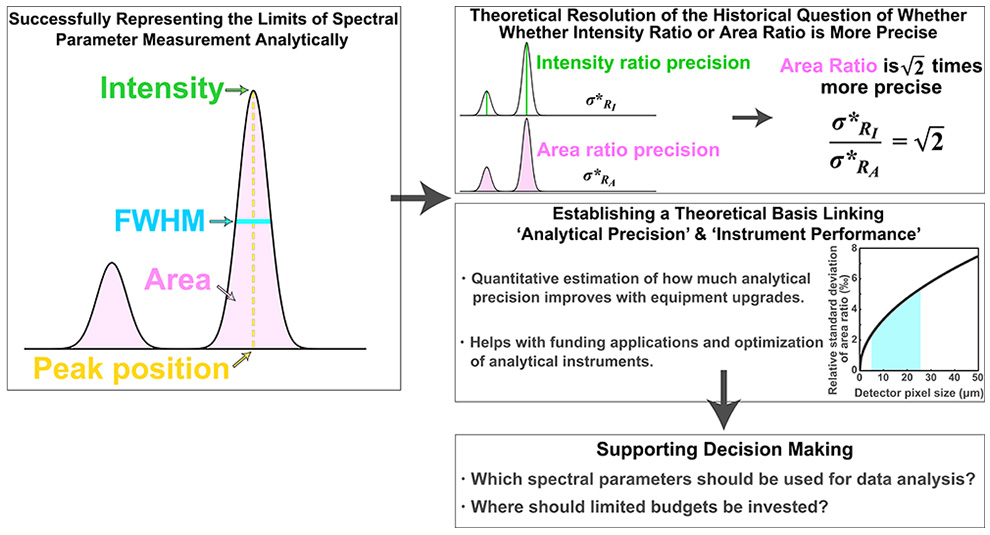
Figure 1　Overview of this study.

2. Overview

Yuuki Hagiwara, a researcher in the Solid Earth Geochemistry Research Group, and Tatsu Kuwatani, a senior researcher in the Data Science Research Group, both at the Volcanoes and Earth’s Interior Research Center, Institute for Marine Geodynamics, Japan Agency for Marine-Earth Science and Technology (President: Hiroyuki Yamato, hereinafter referred to as "JAMSTEC"), have provided a theoretical answer to a long-debated issue in analytical chemistry. The issue concerns which estimator, the intensity ratio or area ratio, provides a more precise prediction of concentrations from spectral data. In this study, based on the Cramér-Rao inequality^※1, we derived an analytical solution representing the limits of spectral parameter measurement and proved that the area ratio is √2 times more precise than the intensity ratio. Previously, experimental results showing higher precision for the area ratio were attributed to the area being an integral of intensity and thus containing more information. However, our study demonstrates that the superior precision of the area ratio is due to the negative covariance between intensity and the full width at half maximum (FWHM).

Furthermore, by combining the analytical solutions for the limits of spectral parameter measurement with insights from spectroscopy, we established a theoretical framework linking "analytical precision" with "instrument performance." This theoretical framework allows us to numerically determine which components of an instrument should be upgraded to efficiently improve analytical precision. These numerical calculations can provide compelling justification when applying for funding to update equipment and enable the most effective improvements within a limited budget. The analytical solutions for measurement limits obtained in this study not only aid in optimizing analytical systems but also serve as theoretical benchmarks for evaluating the performance of new data processing algorithms and analytical protocols. These findings are expected to significantly contribute to the advancement of analytical chemistry.

These findings were published in "Scientific Reports" on October 15(Japan Time). This research was supported by JST CREST (JPMJCR1761) and JSPS KAKENHI (JP19J21537 and JP22J00081).

3. Background

For analytical chemists, achieving maximum precision with minimal sample usage is a critical goal. To efficiently achieve this goal, understanding the physical and statistical background governing analytical precision is essential. In many fields of science and engineering, including analytical chemistry, spectral data are collected to estimate physicochemical properties of substances using parameters such as peak intensity, area, peak position, and full width at half maximum (FWHM). Specifically, intensity ratios and area ratios are key indicators of substance concentrations. For applications such as environmental monitoring of trace element ratios or isotope ratios, where small concentration variations must be detected, these ratios need to be estimated with high precision. Therefore, the question of whether the intensity ratio or area ratio is more precise, and how to effectively improve their precision within a limited budget, has been experimentally investigated since at least the 1960s.

However, previous studies have not provided a consistent quantitative answer. This inconsistency is due to various external factors affecting experiments, such as noise, spectral distortion, instrument performance, and uncertainties in estimating population variance. It is evident that simulations and theoretical approaches are effective in eliminating these external factors, but such approaches have not been undertaken until now.

4. Outcome

Estimating the precision of spectral parameters is critical in various fields of science and engineering, as it significantly influences decision-making in data analysis and equipment upgrades. To determine which is more precise, the intensity ratio or the area ratio, we first derived an analytical solution for the precision limits of spectral parameters using the Cramér-Rao bound. Furthermore, by combining the Cramér-Rao bound with insights from spectroscopy, we established a theoretical framework linking "analytical precision" to "instrument performance." Finally, to demonstrate how this theoretical framework can guide the optimization of instruments for high-precision analysis, we numerically calculated the improvement in precision achieved through equipment upgrades, using non-destructive local isotopic ratio measurements of CO₂'s carbon isotopes by Raman spectroscopy^※2 as an example.

4.1 Analytical solution for the lower limit of standard deviation of spectral parameters

Based on the concept of the Cramér-Rao bound, we derived the variance-covariance matrix^※3 of spectral parameters (Figure 2).

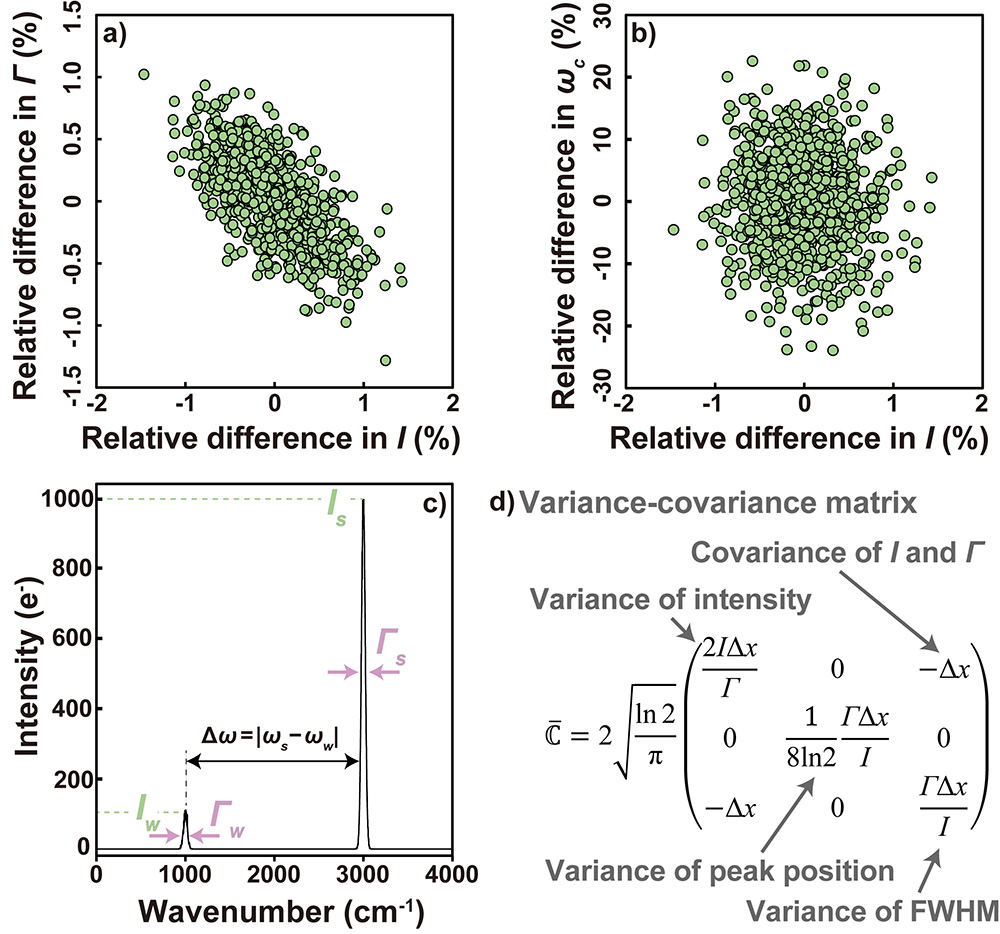
Figure 2　Correlations between (a) intensity and full width at half maximum and (b) intensity and peak position obtained from simulations under the following conditions: Δxs = Δxw = 0.05 cm^-1/pixel, Γs = Γw = 50 cm^-1, Is = 1000 e-, Iw = 100 e-, and Δω = 2000 cm^-1. (c) A typical spectrum generated by the simulation. (d) The variance-covariance matrix of the spectral parameters (θ = (I, ωc, Γ)) derived in this study.

As a result, we found that the lower bounds of the relative standard deviations of peak intensity, position, full width at half maximum (FWHM), and area are expressed by the following equations.

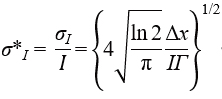	(1)
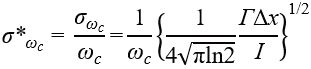	(2)
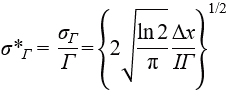	(3)
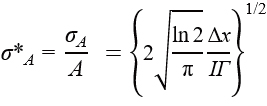	(4)

Here, Δx represents the interval between spectral data points, Γ is the FWHM, and I denotes intensity. From these equations, the following conclusions were drawn:

1. The relative standard deviations of intensity, FWHM, and area are proportional to {Δx/Γ}^1/2. This means that the more data points there are above the FWHM, the better the precision of intensity, FWHM, and area.
2. The precision of intensity, FWHM, and area improves with wider peaks, whereas the precision of peak position is higher for narrower peaks.

Furthermore, calculating the analytical solutions for the relative standard deviations of these differences and ratios yields the following equations.

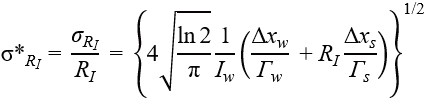	(5)
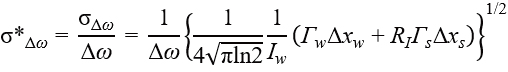	(6)
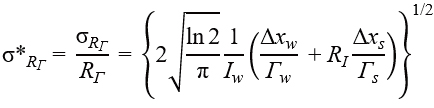	(7)
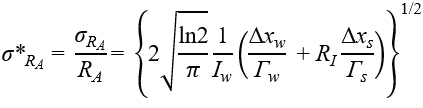	(8)

From these results, taking the ratio of the precision of intensity ratio to area ratio yields the following

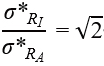(9)

This equation shows that the area ratio is √2 times more precise than the intensity ratio (Figure 3). However, note that this relationship does not hold for all spectra; it depends on the model function and noise model. For instance, if the model function is changed from a Gaussian to a Lorentzian function, the right-hand side of the equation becomes √3 instead of √2.

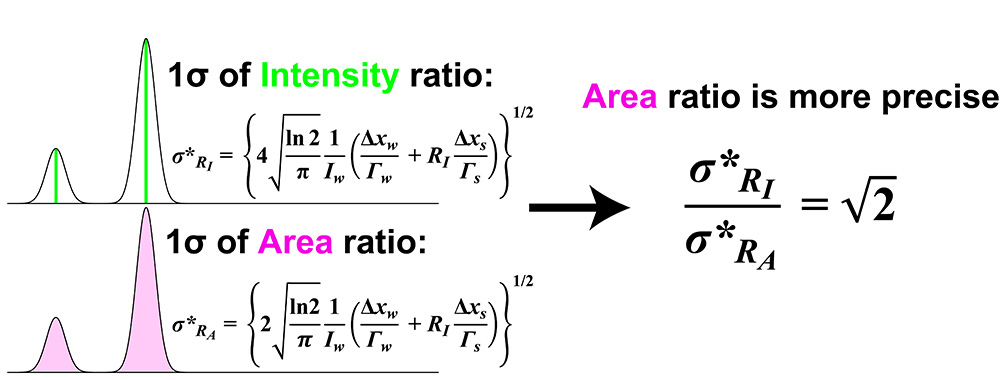
Figure 3　Analytical solution for the lower bounds of the relative standard deviations of the intensity ratio (σ*R_I) and the area ratio (σ*R_A) for peaks approximated by a Gaussian profile under Poisson noise limits, derived based on the Cramér-Rao inequality. Here, I, Γ, Δx, and R_I represent intensity, full width at half maximum, data point interval, and intensity ratio, respectively. The subscripts 'w' and 's' denote the spectral parameters for weak and strong peaks, respectively.

4.2 Why is the area ratio more precise?

As shown in Figures 2a-b, simulation results revealed a clear negative correlation between intensity and full width at half maximum (FWHM). In contrast, there was no correlation between intensity and peak position. This outcome aligns with theoretical calculations, indicating a negative covariance between intensity and FWHM, and zero covariance between intensity and peak position (Figure 2d).

To qualitatively explain why the area ratio is √2 times more precise, the key lies in the negative covariance between intensity and FWHM. Specifically, when the intensity is low, the FWHM tends to be large, and vice versa. As a result, the area, which is proportional to the product of intensity and FWHM, tends to remain stable. Therefore, the superior precision of the area ratio is due to this negative covariance, and the traditional explanation that "the area ratio is more precise because it integrates more intensity information" is not accurate.

4.3 Establishment of a theoretical foundation linking "analytical precision" and "instrumental performance

By expressing the interval between data points (Δx) and FWHM (Γ) in equations 1-8 in terms of instrument performance parameters, we developed a theory linking the precision of spectral parameters to instrument performance (Figure 4). This theoretical framework shows that the relative standard deviation of the area ratio can be expressed as a function of detector pixel size, diffraction grating constant, spectrometer focal length, and wavelength.

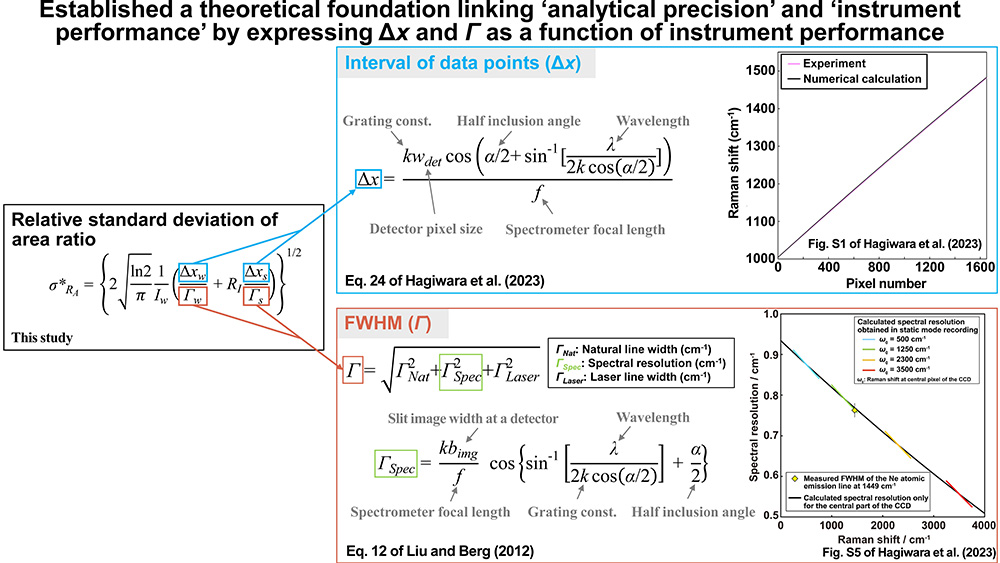
Figure 4　By substituting the interval between spectral data points (Δx) and full width at half maximum (Γ), expressed in terms of instrument performance parameters (such as detector pixel size, diffraction grating constant, and spectrometer focal length), into the analytical solution for the relative standard deviation of the area ratio derived in this study, we established an analytical solution linking analytical precision and instrument performance.

Using this theoretical framework, we numerically calculated how much the precision of non-destructive local isotopic ratio measurements of CO₂'s carbon isotopes using Raman spectroscopy could be improved by upgrading the equipment (Figure 5). This method estimates the isotopic ratio by using the intensity ratio and area ratio of peaks corresponding to ¹²CO₂ and ¹³CO₂ in the Raman spectrum of CO₂. Figure 5 shows how changes in instrument performance affect the measurement precision of the carbon isotopic ratio. The vertical axis represents the relative standard deviation of the area ratio, which corresponds to the standard deviation of the carbon isotopic ratio. The blue region indicates the range of typical instrument performance, and the vertical dotted line represents the performance of the equipment used by Hagiwara et al. (2023).

The figure shows that reducing the detector pixel size from 16 μm to around 5 μm within the blue region significantly improves the measurement precision of the isotopic ratio. Such numerical calculations allow us to quantitatively estimate which components of the equipment should be upgraded to efficiently improve the precision of parameter estimation. This provides compelling justification when applying for funding to upgrade equipment and offers guidance on using research funds more effectively.

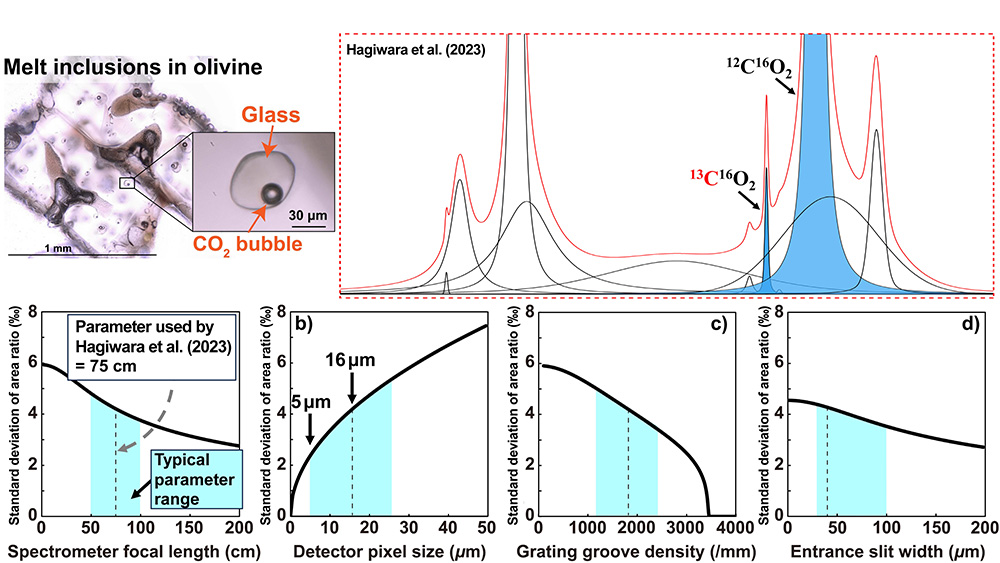
Figure 5　The top right shows the Raman spectrum of CO₂, where the peak intensity ratio and area ratio of ¹²C16O₂ and ¹³C16O₂ can be used to estimate the carbon isotope ratio. This method is being developed to apply to the CO₂ contained in small inclusions captured in volcanic phenocrysts, as shown in the top left photo. The four figures below show the improvement in the relative standard deviation of the area ratio when altering device performance. Specifically, they illustrate the precision changes when varying: (a) the focal length of the spectrometer, (b) the pixel size of the detector, (c) the grating groove density, and (d) the width of the entrance slit.

5．Outlook

In this study, based on the concept of the Cramér-Rao bound, we provided a quantitative answer to the long-standing debate in analytical chemistry about whether the intensity ratio or area ratio is more precise. We found that the area ratio is √2 times more precise than the intensity ratio. Furthermore, by combining the derived analytical solutions for measurement limits with insights from spectroscopy, we established a theoretical framework linking "analytical precision" with "instrument performance."

In this study, we used Raman spectroscopy as an example to establish the theoretical framework linking "analytical precision" with "instrument performance." Moving forward, we plan to collaborate with experts in other analytical techniques to extend this framework, allowing "analytical precision" to be expressed as a function of "instrument performance" in various methods. This approach will enable the optimization of equipment based on the Cramér-Rao bound framework in different fields of analytical chemistry, extending the theoretical foundation to achieve maximum precision with minimal sample across various disciplines.

Furthermore, this study aims to apply non-destructive local carbon isotope ratio measurements of CO₂ to minute inclusions ranging from a few micrometers to several tens of micrometers within volcanic phenocrysts. In fact, using a newly acquired detector with smaller pixel size, based on the theory developed in this study, has significantly improved the measurement accuracy of the carbon isotope ratio. In the future, we aim to apply this method to natural samples to identify the source materials of CO₂ that trigger volcanic eruptions.