１—２．海洋生物地球化学モデル

a. 要約

４成分をもつ簡略な海洋生態系モデルを東大気候センターと地球フロンティアが共同開発する海洋大循環モデルＣＯＣＯに組み込み、７年間の積分を行った結果を観測データと比較した。海洋生態系にとって重要な物理環境である混合層深度は大循環モデルによって比較的よく再現されており、北大西洋北部と南極海における振幅の大きな混合層深度季節変動もモデルによって表現されている。また植物プランクトン現存量の指標となるクロロフィル濃度分布についても、北大西洋・北太平洋北部や赤道域、南極海といったエクマン湧昇域で濃度が高くなる様子、北大西洋北部と南極海における急激な混合層深さの変化のため植物プランクトンのブルームが起こる現象などがモデルにより再現された。炭酸系のモデルへの組み込みも既に完了しており、定常に達するのに必要な数千年の積分をこれから行う予定である。全球の海洋生態系モデルとしては高解像度といえる本研究での設定の下こうした長期積分を行うためには地球シミュレータを用いても３ヶ月程度の実時間が必要であり、従来のスーパーコンピュータでは事実上不可能といえる。

b.研究目的

海洋中の全炭酸鉛直分布は表層付近で濃度が低くなる特徴的な分布をしている。二酸化炭素の大気海洋交換にとって大きな意味を持つこうした分布は生物ポンプ・アルカリポンプ・物理ポンプといった過程によって決定されており、中でも表層生態系における有機物の形成とそれに続く沈降に起因する生物ポンプが最も重要な寄与をなしている。その生物ポンプの効率は、海洋混合層の深さやエクマン湧昇、大気による鉄分の輸送など様々な物理過程から影響を受けている。したがって人為起源二酸化炭素に起因する気候変動が生物ポンプを変化させ、さらに海洋の二酸化炭素吸収に正または負のフィードバックをもたらす可能性は十分にある。

ハドレ−センター（英）やIPSL(仏)が行った陸域−大気−海洋結合炭素循環モデルの結果によれば、気候変動が海洋の二酸化炭素吸収に与える影響は小さいとされる（Cox et al., 2000; Friedlingstein et al. 2001）。しかしながら、大気中の二酸化炭素濃度分布に基づいたインバージョン計算や大気中の窒素／酸素比の観測から算出した海洋二酸化炭素吸収の変動によれば、現在の海洋炭素循環モデルは気候変動に対する感度が鈍いことが示唆されている。大気中二酸化炭素濃度の予測のためには、引き続き海洋炭素循環モデルを改善していくことが必要である。本研究テーマでは、４変数の単純な海洋生態系モデルを炭素循環モデルとともに海洋大循環モデルへ組み込んで海洋炭素循環と気候変化との相互作用を調べ、さらに発展して陸域−大気−海洋結合炭素循環モデルの構築とそれによる全球規模炭素循環の研究を行うことを目的にしている。

c. 研究計画、方法、スケジュール

統合モデル海洋炭素循環コンポーネントに組み込む生態系モデルとしては、Oschlies and Garcon(1999) による植物プランクトン、硝酸、動物プランクトン、デトライタスを変数とする４コンパートメント表層生態系モデルを考えている(図１)。

図１：採用する海洋生態系モデルの概念図。Nは硝酸、Pは植物プランクトン、Zは動物プランクトン、Dはデトライタスをそれぞれ表す。

3年目以降は、この結合モデルを用いた実験及び結果の解析を行う一方、鉄の大気輸送の効果も考慮した最先端のモデルを構築していくことを考えている。鉄の効果を取り入れた海洋生態系モデルは既にいくつか開発されてきており（e.g., Leonard et al., 1999; Archer and Johnson 2000; Moore et al, 2002）、それらを参考に我々のモデルを作り変えていくのは十分可能であると考えられる。また鉄分の大気輸送に関しては、研究実施者の一人が開発したダスト輸送モデルが大気大循環モデルにすぐ組み入れられる形で既に存在する。これらを組み合わせることで大気による鉄分輸送が生物ポンプに与える影響を陽に取り扱えるようになり、氷期−間氷期サイクルや地球温暖化に関して提案されている鉄を介したフィードバック機構（Kumar et al. 1995）に関しより具体的な議論ができるようになると期待される。

d. 平成１４年度研究計画

海洋炭素循環に関して、地球温暖化予測領域で進められている詳細な生物・地球化学過程（１０以上の成分）を含むモデルの開発を進める傍ら、統合モデルに適切な、より簡略なプロセス（４成分程度）を含むモデルをつくり、東大気候センターで開発された海洋モデルＣＯＣＯの中解像度版に導入する作業に着手する。

e. 平成１４年度研究成果

COCOへの海洋生態系モデルの組み込みを終え、モデルによる予備的の結果と観測との比較を行った（図２〜図４）。比較結果は「f. 考察」で述べることとし、以下にはモデルの概略を記す。

前述のように、生態系モデルとしては Oschlies and Garcon (1999) のものを用いる。このモデルは硝酸（Ｎ）、植物プランクトン（Ｐ）、動物プランクトン（Ｚ）、デトライタス（Ｄ）の４つを予報変数として持ち、それぞれの現存量は窒素ベースで表される。変数の時間発展は移流拡散方程式に変数間の相互作用を表すソースシンク項を加えたもので記述される。モデルのパラメータ値には基本的に Oschlies and Garcon (1999) と同一のものを与える。ただしデトライタスの沈降と光合成速度の取り扱いには修正を加えた。Oschlies and Garcon (1999) は全層で一定の沈降速度 5m/d を与えていたが、ここでは表層 150m まで沈降速度 5m/d で沈降し、それより深いところでは Martin (1987) が提唱した曲線に従ってデトライタス沈降フラックスの鉛直方向に分布するとした。また Oschlies and Garcon (1999) が採用していた Eppley (1972) による光合成速度の温度依存性について、20℃ 以上の領域では温度依存性はないものとした。大気−海洋間二酸化炭素交換の際のピストン速度については、Wanninkhof (1992) が定式化したものを用いた。炭酸カルシウム殻の沈降過程については、デトライタスについてのものと同様に取り扱った。

海洋大循環モデルＣＯＣＯの水平解像度は東西ともに１°、鉛直の層数は５４とした。うち表層１００ｍに２０層、１００ｍ深から２００ｍ深までに１０層おくことにした。混合層モデルとして Mellor and Yamada (1974) の level 2 のクロージャスキームを用いている。風応力や海面熱・淡水フラックス、日射といった表面境界条件については OMIP (Ocean Model Intercomparison Project, http://www.clivar.org/organization/wgomd/pomip.htm) により配布されているものを採用した。

モデルを積分する際の初期値には、硝酸については Conkright (1998) による気候値データを用いた。植物プランクトンや動物プランクトン、デトライタスについては全層で 0.1 mmol/m3 とした。全炭酸とアルカリ度については栄養塩のような気候値データセットが今のところ存在しないため、全層一様に一定値2000 mol/m3 を与えた。これらの変数は自然界では鉛直・水平方向ともに有意な分布を持ち、ここでの実験のように積分期間が短い場合に全層に一定値を与えることは本来受け入れがたい設定ではあるが、予備的実験としては十分であろう。大循環モデルに対しては、生態系モデルと結合せずに一万年積分し定常状態に達した場を与え初期値とした。以上の初期値から７年分積分を行い、得られた７年目についての解析結果を次節に示す。

f. 考察

２−４月（ＦＭＡ）	５−７月（ＭＪＪ）
８−１０月（ＡＳＯ）	１１−１月（ＮＤＪ）

２−４月（ＦＭＡ）	５−７月（ＭＪＪ）
８−１０月（ＡＳＯ）	１１−１月（ＮＤＪ）

図２：混合層深度の季節変動。モデル結果 (a) と気候値データ (b) 。単位は m。

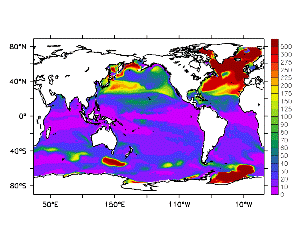
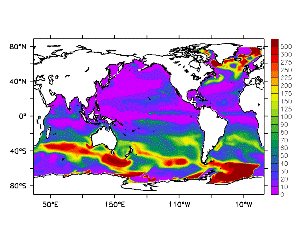
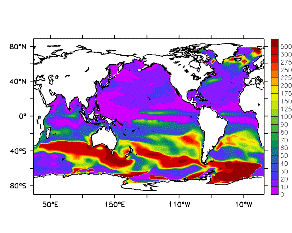
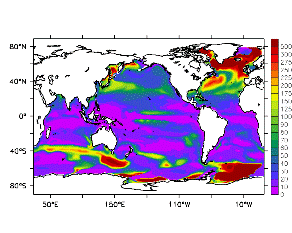
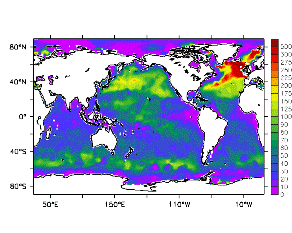
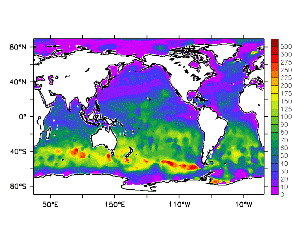
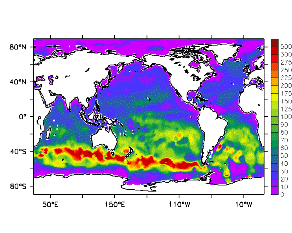
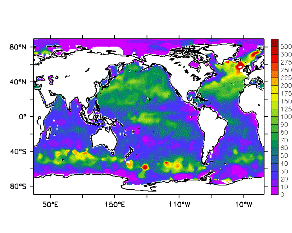
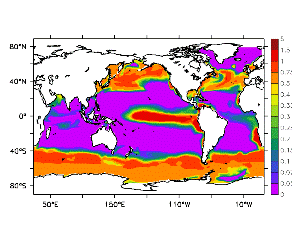
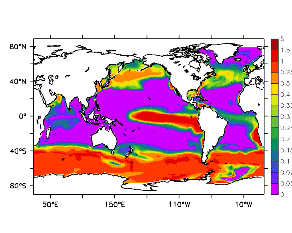
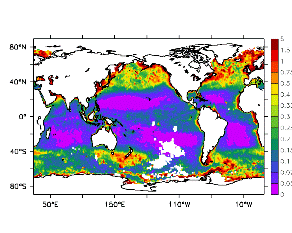
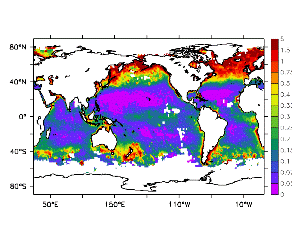
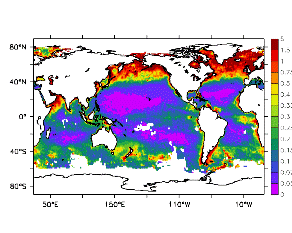
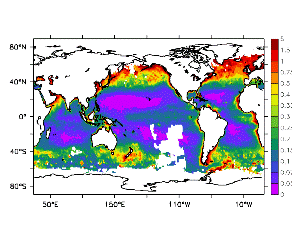
大循環モデルが再現する混合層の深さは、植物プランクトンの光環境と栄養塩環境を規定するため生態系モデルにとって重要なファクターである。図２では、混合層の季節変化についてモデルと観測との比較を行っている。ここで混合層の定義は、海面に対する密度差が水温にして 0.5 度に対応する値に達する深さ、とした。観測の混合層は、Conkright et al. (1998) の水温・塩分のデータをもとに計算した。また海水温の季節変動は大気のそれに比べ２ヶ月程度位相が遅れるため、季節節区分は２−４月を北半球の冬（南半球の夏、ＦＭＡと呼ぶ）と定義し以下３ヶ月ごとに北半球の春・夏・秋（南半球の秋・冬・春、それぞれＭＪＪ・ＡＳＯ・ＮＤＪ）と定義した。ＦＭＡで北大西洋北部に、ＡＳＯで南極海に５００ｍ程度まで混合層が深くなる様子をモデルはよく再現していることが分かる。しかしながらモデル結果において混合層がより深くなっており、かつ混合層が深い領域の面積も大きくなっている。これは一部にはモデルにおいて水温と塩分の鉛直分布が補償しあって鉛直一様な密度分布が形成されているためであり、必ずしもモデルにおいて混合の及ぶ範囲が深すぎることを示すものではない。モデルにおいて混合の及ぶ範囲を忠実に表すためには鉛直拡散係数を基準に混合層の深さを定義するのが望ましいが、観測データから計算する混合層深さとの対応を考えここでは上記の定義を採用した。

図３には植物プランクトン現存量の指標となる海面クロロフィル濃度の季節変動を、モデル結果と衛星観測（ＣＺＣＳ）について示している。なおモデル結果からクロロフィル濃度を得るには一定の換算比 1.59 (mg/m3)/(mmol/m3) を使用した。年間を通じて北大西洋・北太平洋北部、赤道域、南極海で濃度が高い様子がモデルでよく再現されている。これはこれらの海域ではエクマン湧昇のため下層からの栄養塩供給が盛んなためである。また、北大西洋北部で混合層が急激に浅くなるＭＪＪにおいて光環境が改善されクロロフィル濃度が急激に高くなるブルーム現象がモデルでも捉えられていることが分かる。モデルと観測との違いで最も目立つのは赤道域での過大評価であるが、これは他の大規模スケール海洋生態系モデルにも共通して見られるバイアスであり（Fasham et al., 2001）、その除去にはこれから時間をかけて取り組んでいく必要がある。

図４には、通年積分した大気−海洋二酸化炭素交換量を示した。積分期間が７年と短いためモデル結果は初期値に強く依存する。全炭酸とアルカリ度を全球で一様に与えた本実験の結果は科学的に見てそれほど意義のあるものではないが、モデルの開発段階を示すものとして意味はあろう。以後、定常に達するのに必要な数千年の積分を行う予定である。海洋生態系モデルを結合した上で大循環モデルを積分する際には Bryan (1969) の加速法を用いることができず、長期積分には多大な計算資源が必要とされる。本実験における設定で数千年の積分を行うには地球シミュレータを用いても３ヶ月以上の実時間がかかると予想され、従来のスーパーコンピュータで行うことは事実上不可能である。地球シミュレータを用いることにより海洋炭素循環の理解に対し多大な貢献が期待できる。

２−４月（ＦＭＡ）	５−７月（ＭＪＪ）
８−１０月（ＡＳＯ）	１１−１月（ＮＤＪ）

２−４月（ＦＭＡ）	５−７月（ＭＪＪ）
８−１０月（ＡＳＯ）	１１−１月（ＮＤＪ）

図３：海面クロロフィル濃度の季節変動。
モデル結果 (a) とＣＺＣＳによる衛星観測 (b)。単位は mg/m3。

g. 引用文献

h. 成果の発表