JAMSTEC > Research Institute for Value-Added-Information Generation (VAiG) > Center for Mathematical Science and Advanced Technology (MAT) > Member > Yoji Kawamura
Members
Yoji Kawamura
Senior Researcher
Center for Mathematical Science and Advanced Technology
Japan Agency for Marine-Earth Science and Technology
3173-25 Showa-machi, Kanazawa-ku, Yokohama, Kanagawa 236-0001, Japan
ykawamura
researchmap
Short CV
Keywords: Nonlinear Dynamics, Synchronization, Oscillation
Employment
| 2017.4 - | Senior Researcher, Japan Agency for Marine-Earth Science and Technology |
| 2007.4 - 2017.3 | Researcher, Japan Agency for Marine-Earth Science and Technology |
Education
| 2004.4 - 2007.3 | Doctor, Department of Physics, Graduate School of Science, Kyoto University |
| 2002.4 - 2004.3 | Master, Department of Physics, Graduate School of Science, Kyoto University |
| 1998.4 - 2002.3 | Bachelor, Faculty of Science, Kyoto University |
Grants
| 2025.4 - 2030.3 | JSPS KAKENHI Grant Number 25K01160 (Co-I) |
| 2025.4 - 2028.3 | JSPS KAKENHI Grant Number 25K07350 (Co-I) |
| 2024.4 - 2028.3 | JSPS KAKENHI Grant Number 24K06910 (PI) |
| 2020.4 - 2024.3 | JSPS KAKENHI Grant Number 20K03797 (PI) |
| 2018.4 - 2022.3 | JSPS KAKENHI Grant Number 18H03205 (Co-I) |
| 2017.4 - 2021.3 | JSPS KAKENHI Grant Number 17H03279 (Co-I) |
| 2016.4 - 2020.3 | JSPS KAKENHI Grant Number 16K17769 (PI) |
| 2013.4 - 2016.3 | JSPS KAKENHI Grant Number 25800222 (PI) |
Awards
| 2016.3 | Young Scientist Award of the Physical Society of Japan |
| 2015.4 | JAMSTEC Research and Development Achievement Award |
Research Topics
- Phase description approach to synchronization of oscillatory convection
- Phase synchronization between a pair of weakly coupled rotating annuli exhibiting oscillatory convection was experimentally observed. We have thus formulated a theory for the phase description of such oscillatory convection toward a unified understanding of synchronization phenomena in weakly coupled systems of oscillatory convection.
-
Snapshots of the temperature field (T) and phase sensitivity (Z). The phase sensitivity function quantifies the phase response of the oscillatory convection to weak perturbations applied at each spatial point. [Kawamura and Nakao, Chaos 23, 043129 (2013); Phys. Rev. E 89, 012912 (2014).]
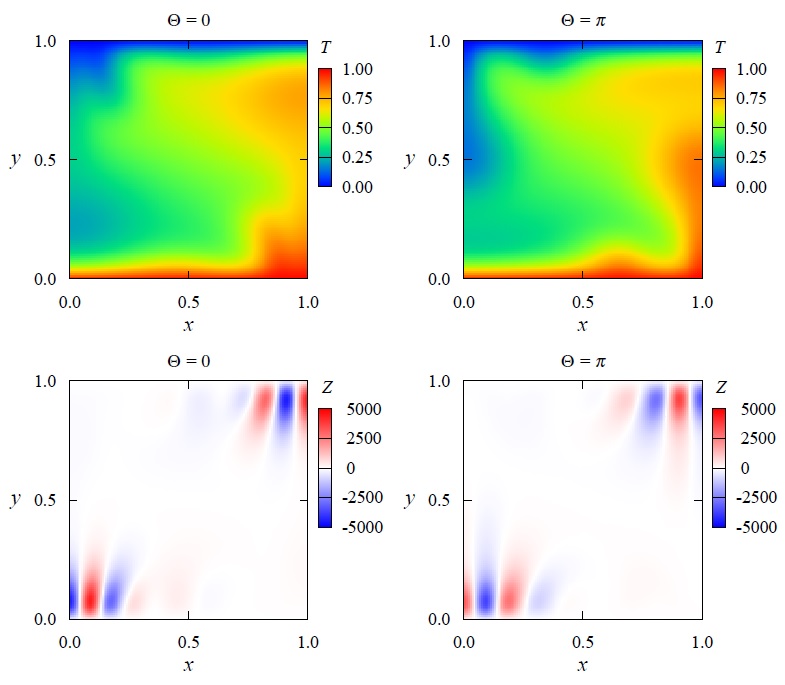
-
Snapshots of the temperature field (T) and two phase sensitivity functions (Zs, Zt). The two phase sensitivity functions quantify the spatiotemporal phase responses of the oscillatory convection to weak perturbations applied at each spatial point. [Kawamura and Nakao, Physica D 295-296, 11-29 (2015).] [Kawamura, Phys. Rev. Research 1, 033130 (2019).] [Twitter, Phase reduction of limit-torus.]
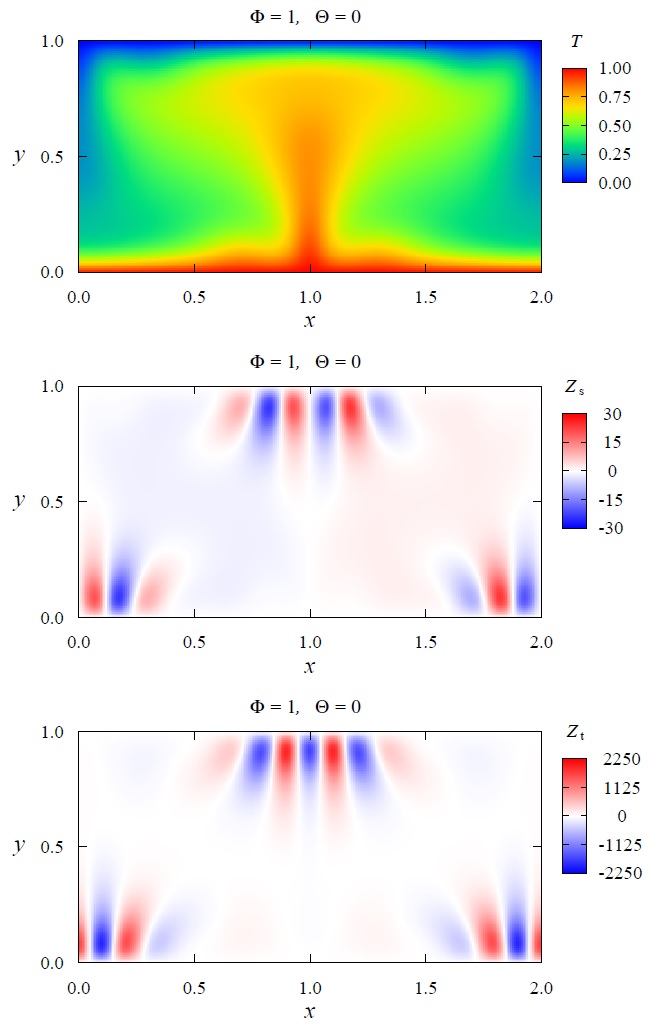
- Phase description approach to synchronization of beating flagella
- Phase synchronization between a pair of hydrodynamically coupled beating flagella was experimentally observed. We have thus formulated a theory for the phase description of such a beating flagellum toward a unified understanding of synchronization phenomena in hydrodynamically coupled beating flagella.
-
Snapshots of the waveform (h) and phase sensitivity (Z). The phase sensitivity function quantifies the phase response of the beating flagellum to weak perturbations applied at each point. [Kawamura and Tsubaki, Phys. Rev. E 97, 022212 (2018).] [Kawamura, Results Phys. 25, 104261 (2021).]
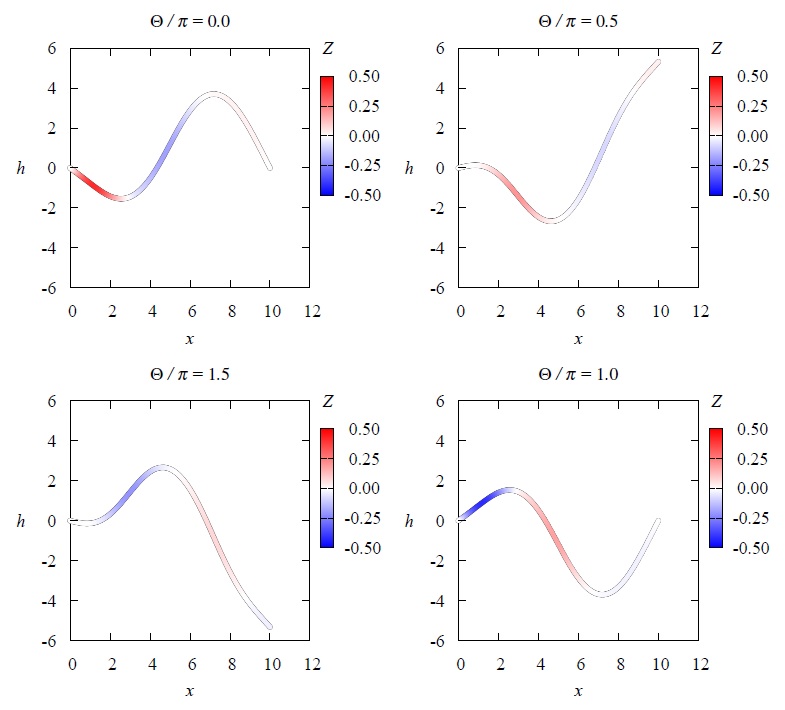
- Phase description approach to synchronization of Karman vortex streets
- We have formulated a theory for the phase description of a Karman vortex street toward a unified understanding of synchronization phenomena of Karman vortex streets.
-
An overview of phase description approach to the Karman vortex street around a circular cylinder. Definition of phase on the basis of the lift coefficient and its time derivative. Snapshots of the vorticity (ω) and phase sensitivity (Zu, Zv) associated with the flow velocity (u, v). The phase sensitivity function quantifies the phase response of the Karman vortex street to weak perturbations applied at each point. [Kawamura, Godavarthi, and Taira, Phys. Rev. Fluids 7, 104401 (2022).] [Godavarthi, Kawamura, and Taira, J. Fluid Mech. 976, R1 (2023).]
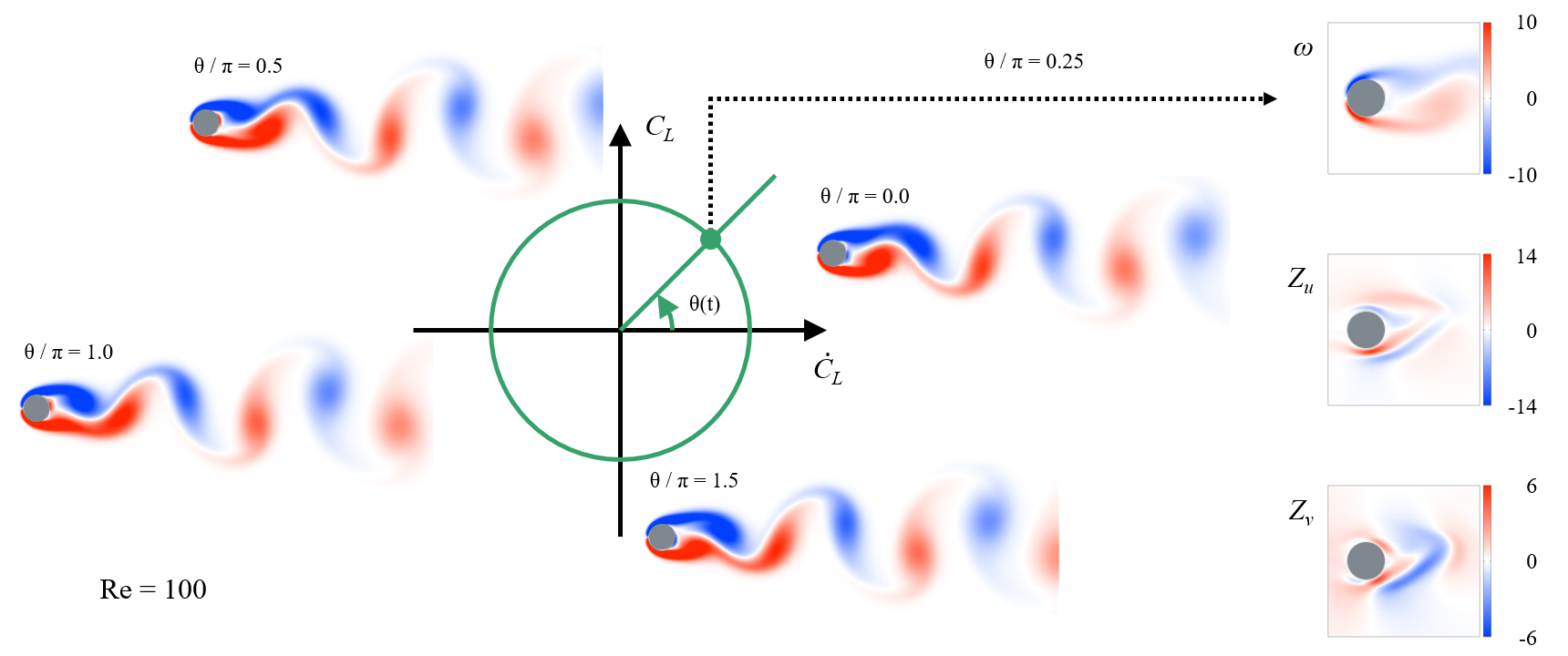
Publications
Original Publications (Peer-Reviewed)
- Takahiro Arai, Yoji Kawamura, Phase reduction analysis of traveling breathers in reaction-diffusion systems, Physical Review Research, 7, 4, 1-20, 043079, (2025), doi:10.1103/4nzq-9kr2
- Shigenobu Hirose, Peter Z. Takacs, Valeriy V. Yashchuk, Keiko Munechika, Yoji Kawamura, Kenji Oguni, Yasushi Hoshino, Katsuhiko Suzuki, Simon Rochester, Topography restoration in white-light interferometry using an instrument transfer function evaluated with binary pseudo-random arrays, Applied Optics, 64, 19, 5461-5477, (2025), doi:10.1364/AO.562002
- Ippei Oshima, Yoji Kawamura, Synchronization phenomenon of temperature oscillation in rotating fluid annulus and optimal waveforms of external forcing, Chaos, 35, 4, 1-14, 043116, (2025), doi:10.1063/5.0233789
- Takahiro Arai, Yoji Kawamura, Toshio Aoyagi, Setting of the Poincare section for accurately calculating the phase of rhythmic spatiotemporal dynamics, Physical Review E, 111, 1, 1-23, 014205, (2025), doi:10.1103/PhysRevE.111.014205
- Vedasri Godavarthi, Yoji Kawamura, Kunihiko Taira, Optimal waveform for fast synchronization of airfoil wakes, Journal of Fluid Mechanics, 976, 1-12, R1, (2023), doi:10.1017/jfm.2023.929
- Sebastian Baum, Patrick Stengel, Natsue Abe, Javier F. Acevedo, Gabriela R. Araujo, Yoshihiro Asahara, Frank Avignone, Levente Balogh, Laura Baudis, Yilda Boukhtouchen, Joseph Bramante, Pieter Alexander Breur, Lorenzo Caccianiga, Francesco Capozzi, Juan I. Collar, Reza Ebadi, Thomas Edwards, Klaus Eitel, Alexey Elykov, Rodney C. Ewing, Katherine Freese, Audrey Fung, Claudio Galelli, Ulrich A. Glasmacher, Arianna Gleason, Noriko Hasebe, Shigenobu Hirose, Shunsaku Horiuchi, Yasushi Hoshino, Patrick Huber, Yuki Ido, Yohei Igami, Norito Ishikawa, Yoshitaka Itow, Takashi Kamiyama, Takenori Kato, Bradley J. Kavanagh, Yoji Kawamura, Shingo Kazama, Christopher J. Kenney, Ben Kilminster, Yui Kouketsu, Yukiko Kozaka, Noah A. Kurinsky, Matthew Leybourne, Thalles Lucas, William F. McDonough, Mason C. Marshall, Jose Maria Mateos, Anubhav Mathur, Katsuyoshi Michibayashi, Sharlotte Mkhonto, Kohta Murase, Tatsuhiro Naka, Kenji Oguni, Surjeet Rajendran, Hitoshi Sakane, Paola Sala, Kate Scholberg, Ingrida Semenec, Takuya Shiraishi, Joshua Spitz, Kai Sun, Katsuhiko Suzuki, Erwin H. Tanin, Aaron Vincent, Nikita Vladimirov, Ronald L. Walsworth, Hiroko Watanabe, Mineral detection of neutrinos and dark Matter. A whitepaper, Physics of the Dark Universe, 41, 1-53, 101245, (2023), doi:10.1016/j.dark.2023.101245
- Takahiro Arai, Yoji Kawamura, Toshio Aoyagi, Extracting phase coupling functions between collectively oscillating networks from time-series data, Journal of the Physical Society of Japan, 91, 12, 1-14, 124001, (2022), doi:10.7566/JPSJ.91.124001
- Yoji Kawamura, Vedasri Godavarthi, Kunihiko Taira, Adjoint-based phase reduction analysis of incompressible periodic flows, Physical Review Fluids, 7, 10, 1-21, 104401, (2022), doi:10.1103/PhysRevFluids.7.104401
- Yoji Kawamura, Factors determining the relaxation time for elastohydrodynamic synchronization of adjacent beating flagella, Results in Physics, 25, 1-6, 104261, (2021), doi:10.1016/j.rinp.2021.104261
- Yoji Kawamura, Stable plane waves in nonlocally coupled phase oscillators, AIP Advances, 11, 1, 1-16, 015304, (2021), doi:10.1063/5.0035637
- Yoji Kawamura, Phase reduction of limit-torus solutions to partial differential algebraic equations, Physical Review Research, 1, 3, 1-23, 033130, (2019), doi:10.1103/PhysRevResearch.1.033130
- Michael Sebek, Yoji Kawamura, Ashley M. Nott, Istvan Z. Kiss, Anti-phase collective synchronization with intrinsic in-phase coupling of two groups of electrochemical oscillators, Philosophical Transactions of the Royal Society A, 377, 2160, 1-15, 20190095, (2019), doi:10.1098/rsta.2019.0095
- Hiroya Nakao, Sho Yasui, Masashi Ota, Kensuke Arai, Yoji Kawamura, Phase reduction and synchronization of a network of coupled dynamical elements exhibiting collective oscillations, Chaos, 28, 4, 1-10, 045103, (2018), doi:10.1063/1.5009669
- Yoji Kawamura, Remi Tsubaki, Phase reduction approach to elastohydrodynamic synchronization of beating flagella, Physical Review E, 97, 2, 1-10, 022212, (2018), doi:10.1103/PhysRevE.97.022212
- Yoji Kawamura, Sho Shirasaka, Tatsuo Yanagita, Hiroya Nakao, Optimizing mutual synchronization of rhythmic spatiotemporal patterns in reaction-diffusion systems, Physical Review E, 96, 1, 1-12, 012224, (2017), doi:10.1103/PhysRevE.96.012224
- Sho Shirasaka, Nobuhiro Watanabe, Yoji Kawamura, Hiroya Nakao, Optimizing stability of mutual synchronization between a pair of limit-cycle oscillators with weak cross coupling, Physical Review E, 96, 1, 1-12, 012223, (2017), doi:10.1103/PhysRevE.96.012223
- Yoji Kawamura, Collective phase reduction of globally coupled noisy dynamical elements, Physical Review E, 95, 3, 1-19, 032225, (2017), doi:10.1103/PhysRevE.95.032225
- Yoji Kawamura, Hiroya Nakao, Optimization of noise-induced synchronization of oscillator networks, Physical Review E, 94, 3, 1-14, 032201, (2016), doi:10.1103/PhysRevE.94.032201
- Yoji Kawamura, Hiroya Nakao, Phase description of oscillatory convection with a spatially translational mode, Physica D, 295-296, 11-29, (2015), doi:10.1016/j.physd.2014.12.007
- Hiroya Nakao, Tatsuo Yanagita, Yoji Kawamura, Phase-reduction approach to synchronization of spatiotemporal rhythms in reaction-diffusion systems, Physical Review X, 4, 2, 1-23, 021032, (2014), doi:10.1103/PhysRevX.4.021032
- Yoji Kawamura, Phase synchronization between collective rhythms of fully locked oscillator groups, Scientific Reports, 4, 1-7, 4832, (2014), doi:10.1038/srep04832
- Yoji Kawamura, Collective phase dynamics of globally coupled oscillators: Noise-induced anti-phase synchronization, Physica D, 270, 20-29, (2014), doi:10.1016/j.physd.2013.12.004
- Yoji Kawamura, From the Kuramoto-Sakaguchi model to the Kuramoto-Sivashinsky equation, Physical Review E, 89, 1, 1-5, 010901(R), (2014), doi:10.1103/PhysRevE.89.010901
- Nozomi Sugiura, Takane Hori, Yoji Kawamura, Synchronization of coupled stick-slip oscillators, Nonlinear Processes in Geophysics, 21, 1, 251-267, (2014), doi:10.5194/npg-21-251-2014
- Yoji Kawamura, Hiroya Nakao, Noise-induced synchronization of oscillatory convection and its optimization, Physical Review E, 89, 1, 1-13, 012912, (2014), doi:10.1103/PhysRevE.89.012912
- Yoji Kawamura, Hiroya Nakao, Collective phase description of oscillatory convection, Chaos, 23, 4, 1-11, 043129, (2013), doi:10.1063/1.4837775
- Hiroya Nakao, Tatsuo Yanagita, Yoji Kawamura, Phase description of stable limit-cycle solutions in reaction-diffusion systems, Procedia IUTAM, 5, 227-233, (2012), doi:10.1016/j.piutam.2012.06.030
- Hiroshi Kori, Yoji Kawamura, Naoki Masuda, Structure of cell networks critically determines oscillation regularity, Journal of Theoretical Biology, 297, 61-72, (2012), doi:10.1016/j.jtbi.2011.12.007
- Yoji Kawamura, Hiroya Nakao, Yoshiki Kuramoto, Collective phase description of globally coupled excitable elements, Physical Review E, 84, 4, 1-12, 046211, (2011), doi:10.1103/PhysRevE.84.046211
- Yoji Kawamura, Hiroya Nakao, Kensuke Arai, Hiroshi Kori, Yoshiki Kuramoto, Phase synchronization between collective rhythms of globally coupled oscillator groups: Noiseless nonidentical case, Chaos, 20, 4, 1-8, 043110, (2010), doi:10.1063/1.3491346
- Yoji Kawamura, Hiroya Nakao, Kensuke Arai, Hiroshi Kori, Yoshiki Kuramoto, Phase synchronization between collective rhythms of globally coupled oscillator groups: Noisy identical case, Chaos, 20, 4, 1-10, 043109, (2010), doi:10.1063/1.3491344
- Naoki Masuda, Yoji Kawamura, Hiroshi Kori, Collective fluctuations in networks of noisy components, New Journal of Physics, 12, 9, 1-15, 093007, (2010), doi:10.1088/1367-2630/12/9/093007
- Naoki Masuda, Yoji Kawamura, Hiroshi Kori, Impact of hierarchical modular structure on ranking of individual nodes in directed networks, New Journal of Physics, 11, 11, 1-21, 113002, (2009), doi:10.1088/1367-2630/11/11/113002
- Naoki Masuda, Yoji Kawamura, Hiroshi Kori, Analysis of relative influence of nodes in directed networks, Physical Review E, 80, 4, 1-10, 046114, (2009), doi:10.1103/PhysRevE.80.046114
- Hiroshi Kori, Yoji Kawamura, Hiroya Nakao, Kensuke Arai, Yoshiki Kuramoto, Collective-phase description of coupled oscillators with general network structure, Physical Review E, 80, 3, 1-9, 036207, (2009), doi:10.1103/PhysRevE.80.036207
- Yoji Kawamura, Hiroya Nakao, Kensuke Arai, Hiroshi Kori, Yoshiki Kuramoto, Collective phase sensitivity, Physical Review Letters, 101, 2, 1-4, 024101, (2008), doi:10.1103/PhysRevLett.101.024101
- Hiroya Nakao, Kensuke Arai, Yoji Kawamura, Noise-induced synchronization and clustering in ensembles of uncoupled limit-cycle oscillators, Physical Review Letters, 98, 18, 1-4, 184101, (2007), doi:10.1103/PhysRevLett.98.184101
- Yoji Kawamura, Hole structures in nonlocally coupled noisy phase oscillators, Physical Review E, 76, 4, 1-4, 047201, (2007), doi:10.1103/PhysRevE.76.047201
- Yoji Kawamura, Chimera Ising walls in forced nonlocally coupled oscillators, Physical Review E, 75, 5, 1-6, 056204, (2007), doi:10.1103/PhysRevE.75.056204
- Yoji Kawamura, Hiroya Nakao, Yoshiki Kuramoto, Noise-induced turbulence in nonlocally coupled oscillators, Physical Review E, 75, 3, 1-17, 036209, (2007), doi:10.1103/PhysRevE.75.036209
- Yoshiki Kuramoto, Yoji Kawamura, External noise can cause complex effective dynamics in pattern-forming systems, Journal of the Korean Physical Society, 50, 1, 170-177, (2007), doi:10.3938/jkps.50.170
- Yoji Kawamura, Yoshiki Kuramoto, Phase transition in chemical turbulence through global feedback: Relevance to catalytic CO oxidation on Pt surfaces, Progress of Theoretical Physics Supplement, 161, 216-219, (2006), doi:10.1143/PTPS.161.216
- Yoji Kawamura, Yoshiki Kuramoto, Onset of collective oscillation in chemical turbulence under global feedback, Physical Review E, 69, 1, 1-5, 016202, (2004), doi:10.1103/PhysRevE.69.016202
Other Publications
- Shigenobu Hirose, Patrick Stengel, Natsue Abe, Daniel Ang, Lorenzo Apollonio, Gabriela R. Araujo, Yoshihiro Asahara, Laura Baudis, Pranshu Bhaumik, Nathaniel Bowden, Joseph Bramante, Lorenzo Caccianiga, Mason Camp, Qing Chang, Jordan Chapman, Reza Ebadi, Alexey Elykov, Anna Erickson, Valentin Fondement, Katherine Freese, Shota Futamura, Claudio Galelli, Andrew Gilpin, Takeshi Hanyu, Noriko Hasebe, Adam A. Hecht, Samuel C. Hedges, Shunsaku Horiuchi, Yasushi Hoshino, Patrick Huber, Yuki Ido, Yohei Igami, Yuto Iinuma, Vsevolod Ivanov, Igor Jovanovic, Ayuki Kamada, Takashi Kamiyama, Takenori Kato, Yoji Kawamura, Giti A. Khodaparast, Yui Kouketsu, Yukiko Kozaka, Emilie M. LaVoie-Ingram, Matthew Leybourne, Gavishta Liyanage, Brenden A. Magill, Paolo Magnani, William F. McDonough, Katsuyoshi Michibayashi, Naoki Mizutani, Kohta Murase, Tatsuhiro Naka, Taiki Nakashima, Kenji Oguni, Mariano Guerrero Perez, Noriaki Sakurai, Lukas Scherne, Maximilian Shen, Joshua Spitz, Kai Sun, Katsuhiko Suzuki, Koichi Takamiya, Jiashen Tang, Erwin H. Tanin, Ethan Todd, Atsuhiro Umemoto, Keegan Walkup, Ronald Walsworth, Alexis M. Willson, Norihiro Yamada, Seiko Yamasaki, Wen Yin, Akihiko Yokoyama, Mineral Detection of Neutrinos and Dark Matter 2025 Proceedings, arXiv:2508.20482, 1-75, (2025), doi:10.48550/arXiv.2508.20482
- Sebastian Baum, Patrick Huber, Patrick Stengel, Natsue Abe, Daniel G. Ang, Lorenzo Apollonio, Gabriela R. Araujo, Levente Balogh, Pranshu Bhaumik Yilda Boukhtouchen, Joseph Bramante, Lorenzo Caccianiga, Andrew Calabrese-Day, Qing Chang, Juan I. Collar, Reza Ebadi, Alexey Elykov, Katherine Freese, Audrey Fung, Claudio Galelli, Arianna E. Gleason, Mariano Guerrero Perez, Janina Hakenmüller, Takeshi Hanyu, Noriko Hasebe, Shigenobu Hirose, Shunsaku Horiuchi, Yasushi Hoshino, Yuki Ido, Vsevolod Ivanov, Takashi Kamiyama, Takenori Kato, Yoji Kawamura, Chris Kelso, Giti A. Khodaparast, Emilie M. LaVoie-Ingram, Matthew Leybourne, Xingxin Liu, Thalles Lucas, Brenden A. Magill Federico M. Mariani, Sharlotte Mkhonto, Hans Pieter Mumm, Kohta Murase, Tatsuhiro Naka, Kenji Oguni, Kathryn Ream, Kate Scholberg, Maximilian Shen, Joshua Spitz, Katsuhiko Suzuki, Alexander Takla, Jiashen Tang, Natalia Tapia-Arellano, Pieter Vermeesch, Aaron C. Vincent, Nikita Vladimirov, Ronald Walsworth, David Waters, Greg Wurtz, Seiko Yamasaki, Xianyi Zhang, Mineral Detection of Neutrinos and Dark Matter 2024. Proceedings, arXiv:2405.01626, 1-70, (2024), doi:10.48550/arXiv.2405.01626
- Yoji Kawamura, Theory of phase reduction for oscillatory convection with infinite degrees of freedom, Meeting Abstracts of the Physical Society of Japan, 71, 2986-2987, (2016), doi:10.11316/jpsgaiyo.71.1.0_2986
- Yoji Kawamura, Hierarchical structure and collective phase description of coupled oscillators, RIMS Kokyuroku, 1827, 51-61, (2013), hdl:2433/194783
- Naoki Masuda, Yoji Kawamura, Hiroshi Kori, Effects of network structure on the precision of biological rhythms, Journal of the Japan Society for Precision Engineering, 77, 2, 145-148, (2011), doi:10.2493/jjspe.77.145
- Naoki Masuda, Yoji Kawamura, Hiroshi Kori, Structure of networks determines the system size dependency of noise intensity in collective dynamics, Seibutsu Butsuri, 49, Supplement, S48-S49, (2009), doi:10.2142/biophys.49.S48_5
- Kunihiko Watanabe, Wataru Ohfuchi, Akira Kageyama, Keiko Takahashi, Fumiaki Araki, Kanya Kusano, Shigenobu Hirose, Hideharu Sasaki, Nobumasa Komori, Takeshi Enomoto, Akira Kuwano-Yoshida, Bunmei Taguchi, Mamoru Hyodo, Mikito Furuichi, Takehiro Miyagoshi, Ryo Onishi, Takeshi Sugimura, Yuya Baba, Shin-ichiro Kida, Shintaro Kawahara, Nobuaki Ohno, Akio Kawano, Tooru Sugiyama, Shin-ichiro Shima, Hiroki Hasegawa, Yoji Kawamura, The Earth Simulator Center, JAMSTEC Report of Research and Development, 9, 1, 75-135, (2009), doi:10.5918/jamstecr.9.1_75
- Yoji Kawamura, Hiroya Nakao, Yoshiki Kuramoto, Hierarchical structure of nonlocally coupled oscillator system, NCTAM papers, 57, 223, (2008), doi:10.11345/japannctam.57.0.223.0
- Hiroya Nakao, Kensuke Arai, Yoji Kawamura, Noise-induced synchronization and clustering in ensembles of uncoupled limit-cycle oscillators, Bussei Kenkyu, 87, 4, 546-549, (2007), hdl:2433/110750
- Yoji Kawamura, Hiroya Nakao, Yoshiki Kuramoto, Noise-induced spatiotemporal chaos in nonlocally coupled oscillators, NCTAM papers, 55, 96, (2006), doi:10.11345/japannctam.55.0.96.0
Books and Book Chapters
- Yoshiki Kuramoto, Yoji Kawamura, Science of Synchronization: Phase Description Approach (353 pages) (Kyoto University Press, 2017) [Kyoto University Press] [References] [Google Books]
- Yoshiki Kuramoto, Yoji Kawamura, Mathematical Theory of Synchronization Phenomena: Phase Description Approach (Nonlinear Science Series 6) (293 pages) (Baifukan, 2010) [Google Books]

