物理情報に基づく深層学習と統計解析の組み合わせによる地下構造推定 ―地震の震源過程の不確実性定量化に期待―

1. 発表のポイント
震源過程や震源位置など地震の特徴を知るための地震データ解析においては、地震発生場である地下構造の推定情報が使用される。この関係から地震の特徴を正しく把握するには、地下構造の不確実性を定量化することが不可欠だが、それはこれまで技術的に困難であった。
物理情報に基づく深層学習※1とベイズ推定※2という統計解析手法を組み合わせることで、推定結果の不確実性を定量化できる新たな地下構造推定手法の開発に成功した。
開発した地下構造推定手法は、地震の震源過程の推定をはじめとした、地下構造推定の結果から派生する様々な地震データ解析における不確実性定量化への発展が期待される。
物理情報に基づく深層学習(Physics-Informed Neural Network:PINN):観測データを学習して何らかのパターンを発見しようとする際、データ自体だけでなく、観測データが生成されるプロセスを支配する物理現象を記述した式からの情報も学習に活用する深層学習手法。
ベイズ推定:ベイズの定理に基づく統計的推定手法。ベイズの定理は、ある事象に関連する可能性のある条件についての事前の知識に対し、新しいデータが取り込まれたときの、その事象の確率を記述する。
2. 概要
国立研究開発法人海洋研究開発機構(理事長 大和 裕幸、以下「JAMSTEC」という。)海域地震火山部門地震発生帯研究センターの縣亮一郎研究員、白石和也副主任研究員、藤江剛センター長らは、「物理情報に基づく深層学習」(PINN)を用い、推定結果の不確実性を定量化できる新たな地下構造推定手法を開発しました。
震源過程や震源位置といった地震の特徴を調べるために行われる地震データの解析においては、地震発生場である地下の岩石の地震波速度構造の情報が不可欠です。地下構造は屈折法弾性波探査などを通じて推定されますが、弾性波探査データの質および量の制約からその推定には必ず不確実性を伴う性質があります。地下構造の不確実性がどの程度かということは、地震データの解析により推定される震源過程等の不確実性に直結します。地震の特徴を正しく把握するために、近年様々な分野で広く用いられるベイズ推定などの統計解析手法に基づいて、地下構造推定結果の不確実性を定量的に示すことが重要です。しかしこのような解析は、統計解析にかかる膨大な計算処理などに対処するために、本来の地下構造における物理的に重要な特徴である「連続性」を損なってしまう構造の単純化を行う必要があるなど、技術的な困難がありました。他方、自然科学データの解析のための新たな方法として注目を集めているPINNは、地下構造を連続な分布で表現できるなど従来法にはないメリットをもたらしますが、PINNを用いた解析における不確実性定量化の方法はまだ確立されていませんでした。
本研究では、PINNと、深層学習と相性の良いベイズ推定手法を組み合わせ、不確実性を定量に示すことが可能となる新たな地下構造推定手法を考案しました。PINNの導入により、地下構造の重要な「連続」な分布という物理的特徴を保持したまま、推定結果の不確実性を評価することを可能としました。現実の屈折法弾性波探査を模した数値実験において、本手法の実解析に対する適用可能性を確認しました。このようにPINNを用いた自然科学データの解析において、ベイズ推定による実用的な精度での不確実性の定量化を実用的な問題例で成功させた事例は、地球科学の分野では本研究が世界で初めてです。
これにより、屈折法弾性波探査における地下構造推定結果のみならず、震源位置や震源過程の推定をはじめとした、地下構造推定の結果から派生する様々な地震データ解析における不確実性の把握への扉が開かれることになります。
なお、この研究はJSPS科研費21K14024からの助成を受けました。また、深層ニューラルネットワークの並列学習にJAMSTECの地球シミュレータを使用しました。
本成果は、「IEEE Transactions on Geoscience and Remote Sensing」に10月9日付け(現地時間)で正式版が掲載されました。
Bayesian seismic tomography based on velocity-space Stein variational gradient descent for physics-informed neural network
3. 背景
地下構造(特に地震波速度:地震波が岩石中を伝わる速度)の情報は、地震の発生過程を探るうえでの基礎となります。なかでも、震源過程や震源位置などを推定して地震の特徴を知るために行われる地震データの解析においては、地震発生場である地下構造の情報が不可欠です。地下構造の推定手法の一つに、地表面や海中で人工的に弾性波を発生させ、地下での速度の変化により屈折して戻ってきた屈折波を、地表面や海底の地震計で観測した波形データを用いて観測・処理する屈折法弾性波探査があります(図1)。ただし、弾性波探査データの質・量に限界があることに起因し、推定結果は不確実性を有しており、結果のすべてを信用することはできません。地下構造の推定結果における不確実性がどの程度かということは、それを基礎として行われる地震のデータ解析により推定される震源過程等の不確実性に直結します。このことにより、地震の特徴を正しく把握するためには、地殻構造の不確実性を定量的に示すことが重要だといえます。しかし、これは一般的な地下構造推定手法を用いるだけでは不可能であり、不確実性の定量化が可能となる手法構築・解析を別途行う必要があります。これは従来、比較的単純な統計処理により行われてきました。一方、自然科学の分野では、工学・ビジネスの分野でも広く用いられるベイズ推定と呼ばれる統計学の手法に立脚した不確実性の定量化が主流となりつつあります。ベイズ推定は、過去の知識や予備データからの情報を不確実性の計算に取り込むことができるため、観測データが不十分な問題での使用に適しています。地下構造推定においても同様に、ベイズ推定のアプローチをとることが求められてきています。しかしこのような解析は従来、統計解析にかかる膨大な計算処理などに対処するために、本来の地下構造の「連続性」を損なう単純化を行う必要がありました。連続性は多くの物理的構造に対して重要な特徴であり、地下の物性構造も特徴的な物性境界を除けば連続性を持つと考えられています。
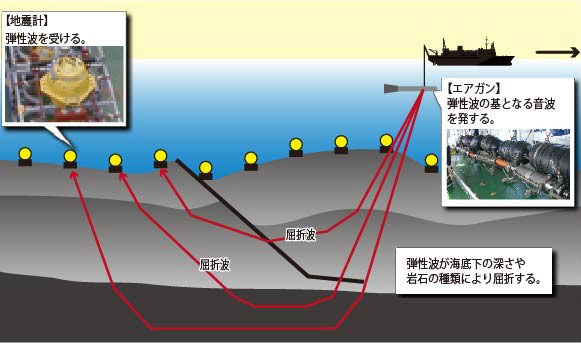
図1.海域における屈折法弾性波探査のイメージ。エアガンから発した波が海底を伝わり、地層の境界面で屈折し、やがて戻ってくる屈折波から地下構造を調べる。
他方、PINNという比較的新しい技術が、自然科学データの解析のための新たな方法として注目を集めています。PINNで使用する深層学習は、最近ではChatGPTをはじめとした大規模言語モデル等の高精度生成AIを実現するなど、ここ十年程度のAI技術の発展において中心的な役割を担う機械学習手法です。従来の数値計算手法では、地下の物性構造のような物理的構造を表現するために、対象となる領域を細かく区切る計算格子・メッシュを用います。PINNは、その代わりに深層ニューラルネットワーク※3を用いて物理的構造を(時)空間的に「連続」な関数で表現できるため、地下構造の連続性を保った解析が可能となります。このPINNの特徴が、地下構造推定に、推定の安定化や計算プロセスの効率化等、従来の数値計算手法にはないメリットをもたらすことが指摘されており、当分野においても発展が期待されています。しかし、PINNとベイズ推定等を組み合わせ、自然科学データの解析における不確実性の定量化を行う研究はまだ発展途上であり、手法がまだ確立されていません。そのため、PINNを用いた屈折法弾性波探査での地下構造推定の実施と、そこでの不確実性定量化による不確実性の担保、の双方を両立させることはまだ難しい状況でした。
深層ニューラルネットワーク:人間の神経細胞とそのつながりを再現したニューラルネットワークを多層化して識別タスク等を行う機械学習の手法の一つ。
4. 成果
本研究では、深層学習に対して相性の良いベイズ推定手法とPINNを世界で初めて組み合わせることで、不確実性の定量化が可能となる新しい地下構造推定を構築しました(図2)。本手法は、制御された人工震源から観測計までの走時(波の到達時刻)データをもとに(図2①)、関数空間粒子ベース変分推論と呼ばれるベイズ推定手法を用い、地下の速度構造とそこでの弾性波の伝わり方を数百の深層ニューラルネットワークに並列学習させます(図2②)。そして、統計処理により多数の学習結果のばらつき(標準偏差等)を見ることで不確実性を定量化します(図2③)。これにより、PINNを用いた屈折法弾性波探査での地下構造推定を、不確実性定量化も含めて実施することが可能となりました。また、PINNに基づく本手法では、図2③に示す速度構造の多数の学習結果において、地下構造の重要な物理的特徴である連続性が保持されています。
図2に示すような理想的な問題に加え、現実の屈折法弾性波探査を模した設定においてもテストを行うことで、本手法の実解析に対する適用可能性も確認することができました(図3)。PINNを用いた自然科学データの解析において、ベイズ推定による実用的な精度での不確実性定量化を、屈折法弾性波探査のような実用的な問題例で成功させた事例は、地球科学の分野では本研究が初めての事例です。
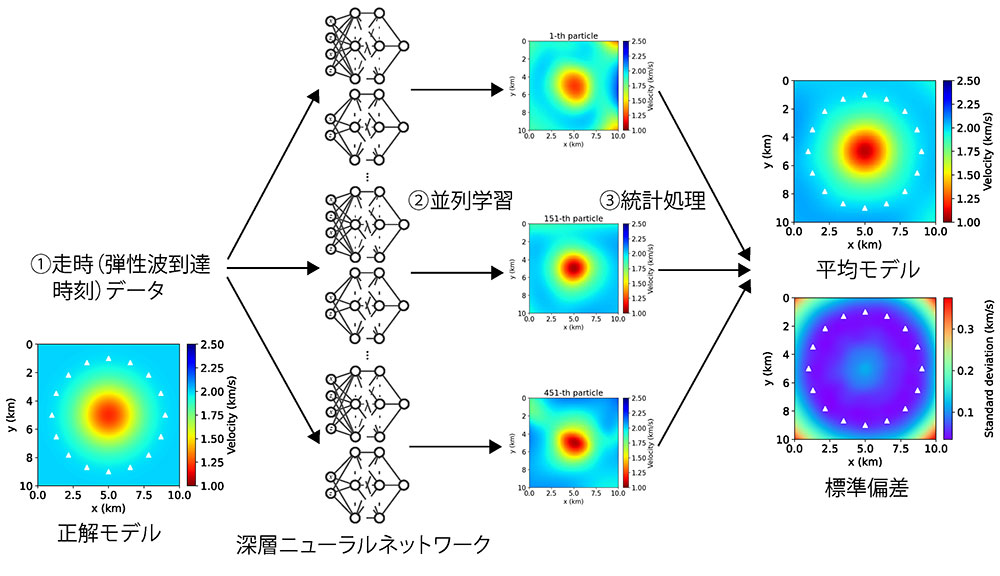
図2.単純なテスト問題を例にした開発手法の概要説明図。①制御された人工震源から観測計までの走時(波の到達時刻)データを推定に用いる。②関数空間粒子ベース変分推論と呼ばれるベイズ推定手法を用い、地下の速度構造とそこでの波の伝わり方を数百組の深層ニューラルネットワークに並列学習させる。ここで、ニューラルネットワーク二つが一組を形成している。③統計処理により多数の学習結果のばらつきを見ることで不確実性を定量化する。
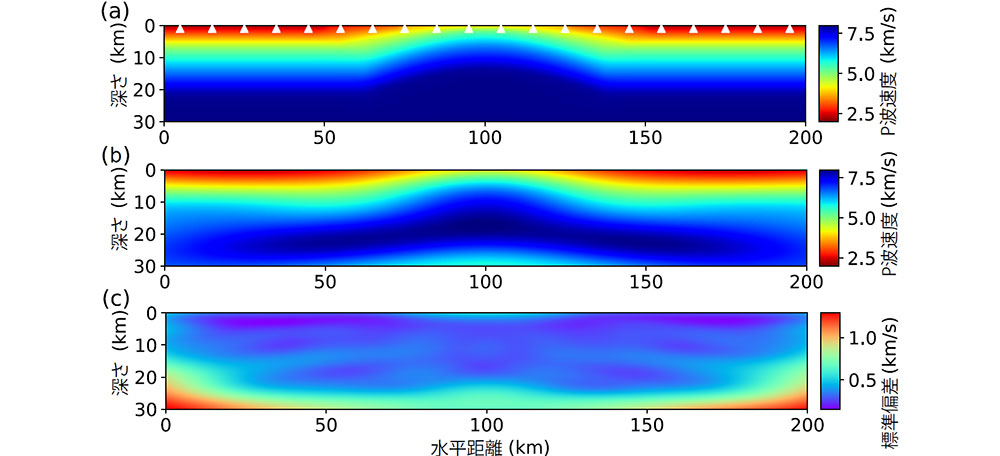
図3.単純なテスト問題を例にした開発手法の概要説明図。①制御された人工震源から観測計までの走時(波の到達時刻)データを推定に用いる。②関数空間粒子ベース変分推論と呼ばれるベイズ推定手法を用い、地下の速度構造とそこでの波の伝わり方を数百組の深層ニューラルネットワークに並列学習させる。ここで、ニューラルネットワーク二つが一組を形成している。③統計処理により多数の学習結果のばらつきを見ることで不確実性を定量化する。
5. 今後の展望
本研究の成果により、PINNの枠組みに基づいた、不確実性を定量化に示すことのできる地下構造推定が可能となりました。屈折法弾性波探査の実データへの適用により、探査による地下構造推定結果の不確実性が定量化され、結果の不確実性を担保できることが期待されます。また、PINNの導入は、地下構造の重要な物理的特徴である連続性を保持したまま、推定結果の不確実性を評価することを可能としました。重要な物理的特徴が保持されていれば、地下構造情報を使用する様々な物理的計算に推定結果を用いることが可能です。このことは、本手法で定量化された地下構造の不確実性が、震源過程や震源位置等の解析をはじめとして、派生する様々な地震データ解析の不確実性にどの程度影響するかを、引き続いて検討できることを意味します。これにより、地震に関わる様々な解析における不確実性の定量的把握への扉が開かれたことにもなり、今後の研究の進展が期待されます。