7章:並列化とベクトル化
7.1 並列化
7.1.1 スーパーコンピュータとは
サイエンスの未知の扉を開くためには、膨大な量の科学計算を、高速に、かつ効率的に処理する必要がある。
スーパーコンピュータは、その時代における最先端の技術を集結し、最も高速な処理能力を有し、構成上も最大のコンピュータ群の総称である。高性能コンピュータ(HPC:High Performance Computer)とも呼ばれる。
スーパーコンピュータとは…
- 大規模な科学技術計算に用いられる超高性能コンピュータ
- その時点での最先端の技術を結集して開発されたコンピュータ
- その世代で最も速く、構成上も最大のコンピュータ
スーパーコンピュータを使った数値シミュレーションで対象物を拡大/縮小あるいは時間を延長/短縮することにより、目に見えないもの、予測できないもの実験不可能なものを目で見、予測し、実験を行うことができる。
7.1.2 スーパーコンピュータの処理速度
FLOPS(フロップス)とは、コンピュータの処理速度を表す単位のことで、スーパーコンピュータなど、大規模なコンピュータシステムの性能指標として用いられることが多い。
FLOPSは、FLoating point number Operations Per Secondの略で、1秒間に実行可能な浮動小数点演算の回数を表している。
- 「1G FLOPS」→1秒間に1G(ギガ)(10億回)の浮動小数点演算を実行
- 「1T FLOPS」→1秒間に1T(テラ)(1兆回)の浮動小数点演算を実行
ハードウェアは、年々目覚しい進歩を遂げている。しかし、膨大な量の科学技術計算をより速く行うためには、高速な処理能力をもつコンピュータを、いかに効率よく稼働させるかを考えなければばらない。
高速化のために重要なこと
各CPUの計算速度
→ 演算の高速化:クロック周波数の高速化
→ 回路の高速化:高集積化・高密度実装
各CPUがすべて同じ速度で計算(怠け者を作らない)
→ 同期と負荷の均等化
データの取り出し・格納
→ メモリとCPUのデータ転送速度(バンド幅)
→ データ幅の増大・アクセス時間の短縮
7.1.3 より速く計算するために~並列化
並列化とは、あるひとつのタスク(計算)を、相互に依存性のない複数の細かいタスクに分割し、それらを複数のプロセッサを使って並列処理することをいう。
単一のプロセッサによって処理を行う逐次処理に比べ、プログラムの実行にかかる時間を大幅に短縮させることができる。
例えば、以下のようなDO文を用いた繰り返し処理は、並列化することによって、効率的に処理することができる。
INTEGER A(1),B(1),C(1)
DO I=1,100
C(I)=A(I)+B(I)
END DO
WRITE(*,*)C
END
★逐次処理の場合
A(1)+B(1) → A(2)+B(2) → A(3)+B(3) → … → A(100)+B(100)
★並列処理の場合
A(1)+B(1) → … → A(25)+B(25)
A(26)+B(26) → … → A(50)+B(50)
A(51)+B(51) → … → A(75)+B(75)
A(76)+B(76) → … → A(100)+B(100)
図)処理のイメージ
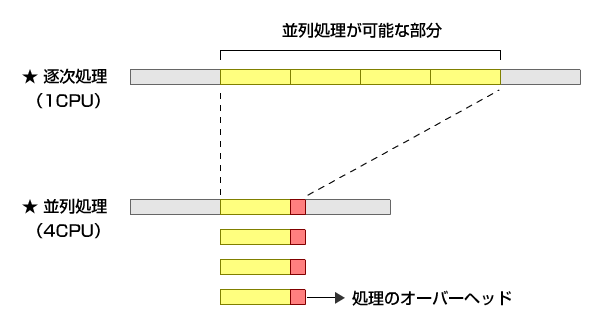
並列化には、コンパイラが自動的にタスク分割をして処理を行う自動並列化と、プログラマが明示的にプログラム内にコード記述を行い並列処理を行う手動並列化がある。この手動並列化には、OpenMP、MPI、HPF等の並列プログラミングモデルがある。
★手動並列化のコード記述方法(OpenMP)★
!$OMP PARALLEL
・・・
・・・ データの処理
・・・
!$OMP END PARALLEL
★例)手動並列化のコード記述★
INTEGER A(1),B(1),C(1)
!$omp parallel do
DO I=1,100
C(I)=A(I)+B(I)
END DO
WRITE(*,*)C
END
ループが入れ子構造になっている場合、なるべく外側のループを並列化した方が、効率がよくなる。これは、スレッドの生成、廃棄の回数を減らすことができるためである。
SUBROUTINE GOUKEI(A,B,C)
REAL(KIND(1.0D0),DIMENSION(N,N),INTENT(IN) A,B
REAL(KIND(1.0D0),DIMENSION(N,N),INTENT(OUT) C
INTEGER I,J
!$omp parallel do ←指示文の直後のループのみ並列化される!
DO I = 1, 100
DO J = 1, 100
C(J,I) = A(J,I) + B(J,I)
END DO
END DO
END SUBROUTINE GOUKEI
並列化できないループ処理もある。
DO I = 2, 100
P(I) = P(I) + P(I - 1)
END DO
上記の例では、p(i)を計算するために、iループの一つ前の値であるp(i-1)を利用するため、並列化によって繰り返しの実行順序が変わると、正常な値が得られなくなってしまう。