The 1000-member ensemble Kalman filtering with the nonhydrostatic numerical weather prediction model on the K computer.
 Summary
SummaryFor improving numerical weather prediction (NWP) for severe phenomena such as local heavy rainfalls and tornados, an accurate initial condition of NWP models is essential in addition to the improvement of NWP models. The initial condition of the NWP model is prepared through the data assimilation process, where the most probable atmospheric state is estimated by optimally coupling numerical model outputs with observations. An ensemble Kalman filter (EnKF) is one of the promising data assimilation techniques, which have been developed to be applied to the NWP in future.
The EnKF is an approximation of the original Kalman filter approach by running a finite number of model forecasts simultaneously and considering each model output as a statistical sample. Although the EnKF has an advantage that a flow-dependent background error covariance can be estimated explicitly in the process, the accuracy of EnKF analyses tends to depend on the number of samples. In realistic EnKF applications for atmospheric data assimilation, the ensemble size is usually no more than 100, which is far fewer than the dimension of the model's sub-space required for a full-scale EnKF. The finite ensemble size introduces a sampling error into the background error covariance, leading to degradation of the accuracy of the analysis fields.
For improving the NWP for severe weather phenomena by improving the data assimilation technique, a 1000-member EnKF with a nonhydrostatic numerical weather prediction model has been implemented on the K computer by Meteorological Research Institute. This is the most extensive numerical experiments for the EnKF data assimilation with a high-resolution NWP model by using the K computer, and can be expected to lead to breakthroughs in data assimilation. Figure 1 shows maps of the horizontal distribution of the error correlation of the horizontal wind at the 500-hPa level. When the error covariance is built up with 50 ensemble perturbations, it has noise patterns at distant locations (Fig. 1a). Horizontal localization suppresses the noise patterns, while the flow dependence around the center point is conserved (Fig. 1b). The error covariance with 1000 members shows a structure similar to that estimated by 50 ensemble members with localization (Fig. 1c). Although the error covariance structure is strongly affected by atmospheric conditions as well as model configurations, Fig. 1c indicates that the amount of 1000 ensemble members might be nearly sufficient to represent the error covariance for horizontal wind without covariance localization techniques. The horizontal cross section of the error correlation of the horizontal wind without localization is shown in Fig. 2. Here, the error correlation is estimated from different numbers of ensemble perturbations in a single experiment with 1000 ensemble members. With small ensemble sizes such as 10 and 20, large spurious noise can be seen, except near the center point. In contrast, the correlation becomes negligible at distant locations with larger ensembles, and correlations built up with 500 and 1000 perturbations show relatively ideal correlation.
The RIKEN has already conducted an EnKF experiment with 10,240 members on the K computer, but using low-resolution atmospheric model and artificial observation data. In this study the EnKF with a large number of ensemble members is implemented with the nonhydrostatic NWP model operationally used in the Japan Meteorological Agency. This is the first trial in the world that investigated the impact of the number of ensemble members on the EnKF with the realistic experimental setting. The results obtained here would contribute to the future development of data assimilation for improving the NWP for severe weather conditions.
The results of this study were presented at “AICS International Workshop on Data Assimilation 2013”, and published in Journal of the Meteorological Society of Japan.
Kunii, M., 2014: The 1000-member ensemble Kalman filtering with the JMA nonhydrostatic mesoscale model on the K computer. J. Meteor. Soc. Japan, 92,
http://dx.doi.org/10.2151/jmsj.2014-607.
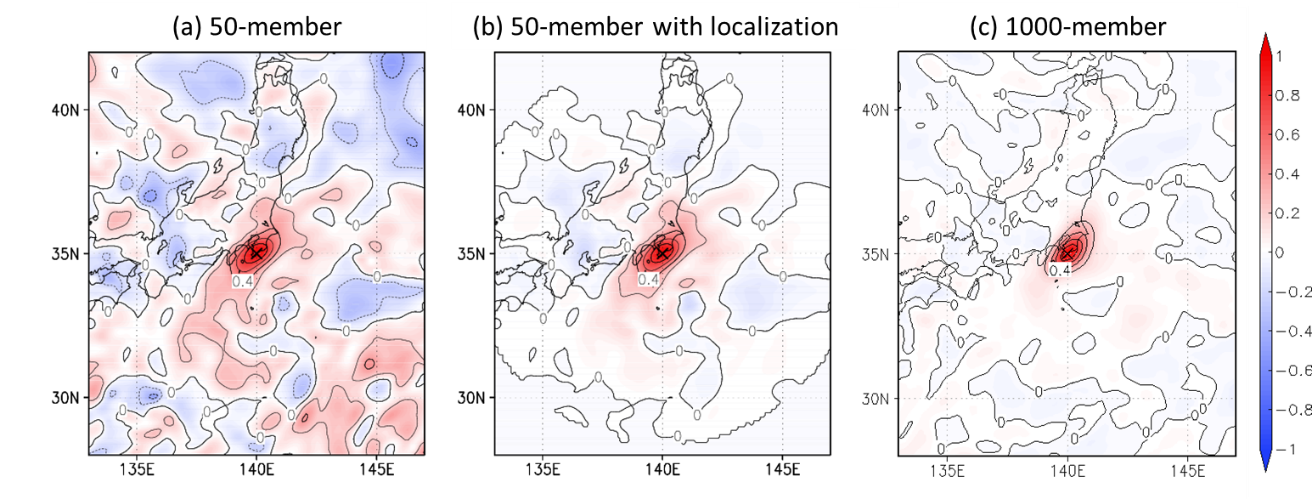
FIG 1. Maps of the horizontal distribution of the error correlation of the horizontal wind at the 500-hPa level from the center location (denoted by the cross marks) estimated from (a) 50 ensemble perturbations without localization, (b) 50 ensemble perturbations with localization, and (c) 1000 ensemble perturbations without localization.
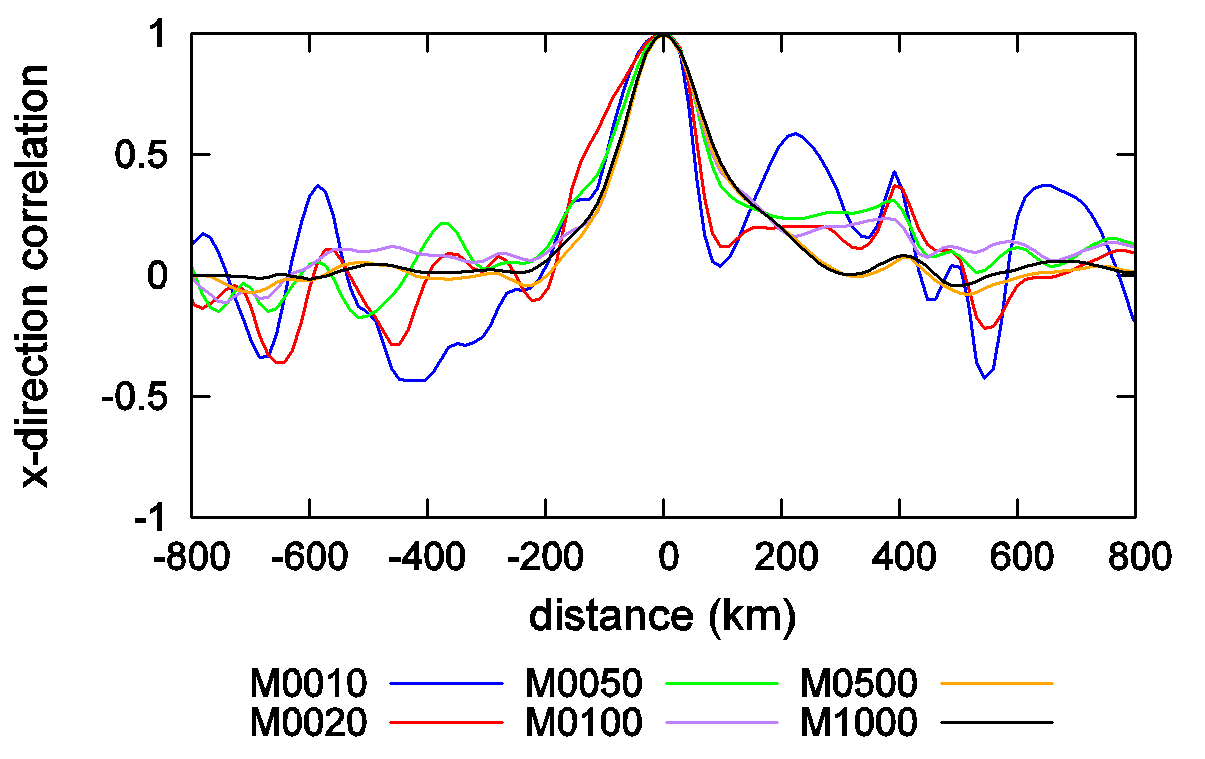
FIG. 2. Horizontal cross section of the horizontal wind error covariance at the 500-hPa level shown in Fig. 2c, estimated from different numbers of ensemble perturbations: 10, 20, 50, 100, 500, and 1000 (After Kunii 2014).
Contacts:
Meteorological Research Institute
Masaru Kunii( )
)
and Kazuo Saito( )
)
Meteorological Research Institute
Masaru Kunii(
 )
)and Kazuo Saito(
 )
)