研究者紹介
エトーレ バルビエリ(Ettore Barbieri)

科学者
国立研究開発法人 海洋研究開発機構
数理科学・先端技術研究開発センター
〒236-0001 神奈川県横浜市金沢区昭和町 3173-25
e.barbieri
Short CV
私の主な研究分野は 破砕力学 に重点を置いて 非線形力学 です。
私が答えようとしている基本的な研究課題は、どのように、いつ、どこで亀裂が伝播するかです。
さまざまな材料(金属、エラストマー、セラミックス、生体材料、複合材料)に対するこれらの答えを得るために、私はその変形を支配する方程式を解くコンピュータプログラムを開発する。
Employment
| 2017.10 - | Scientist at the JAMSTEC Department of Mathematical Science and Advanced Technology (MAT) |
| 2017.10 - | Visiting Senior Lecturer (Associate Professor) School of Engineering and Materials Science (SEMS) Queen Mary University of London, UK |
| 2013.5 - 2017.9 | Lecturer (Assistant Professor) School of Engineering and Materials Science (SEMS) Queen Mary University of London, UK |
| 2010.3 - 2013.4 | Postdoctoral Research Associate Department of Engineering Science University of Oxford, UK |
| 2006.2 - 2007.2 | Research Assistant Department of Aerospace Engineering Università degli Studi di Napoli Federico II, Napoli, Italy |
Education
| 2010.3 - 2007.3 | PhD in Mechanical Engineering University of Bath, UK |
| 2000.10 - 2006.2 | Master in Aerospace Engineering (5-year degree) Università degli Studi di Napoli Federico II, Napoli, Italy |
Research Topics
- 骨折の正確で現実的なシミュレーション
-
右の例では、亀裂の表面が a priori と定義されているため、破損パスは現実的ですが物理的には正確ではありません。
物理的に正確なシミュレーションでは、局所的な応力状態に基づく亀裂進展基準から破断経路が生じる。ストレス状態は、体が経験する緊張から生じる。歪みを得るためには、運動方程式によって支配される変形を計算しなければならない。彼らの解は、しばしば数値的スキームの適用を必要とする。
有限要素法(FEM)のような一般的な数値方法は、(右図のように)亀裂経路を事前に定義するか、時間のかかる再メッシュ化操作を必要とします。
我々の研究では、事前定義または remeshing の両方を避ける、より速い骨折の数値スキームが調査されています。
さらに、正確性と現実性を向上させるために、弾丸やカップなどの衝突中の2つの物体の接触を検出する高速アルゴリズムを研究します。 ([28]、Montanari et al。2017を参照)

弾丸に当たったコーヒーカップの破壊シミュレーション:破砕経路は、断片が分離する表面を先験的に定義する(M. Montanari、Oxford Univ。).
- クラック伝播のためのメッシュフリー方法
-
いくつかのメッシュフリー方法は、変位に対して移動最小二乗(MLS)近似を使用する。 MLSの計算コストを数時間から数分に減らしました(Barbieri and Meo、2012)。亀裂では、身体の変位は不連続でなければなりません。 我々の研究 [9](Barbieri et al。、2012)では、複数の伝播クラックの不連続MLS近似を素早く生成する方法を説明した。 右側に)。
以下では、さまざまな材料で伝播をクラックさせるソフトウェアのアプリケーションを見ることができます。
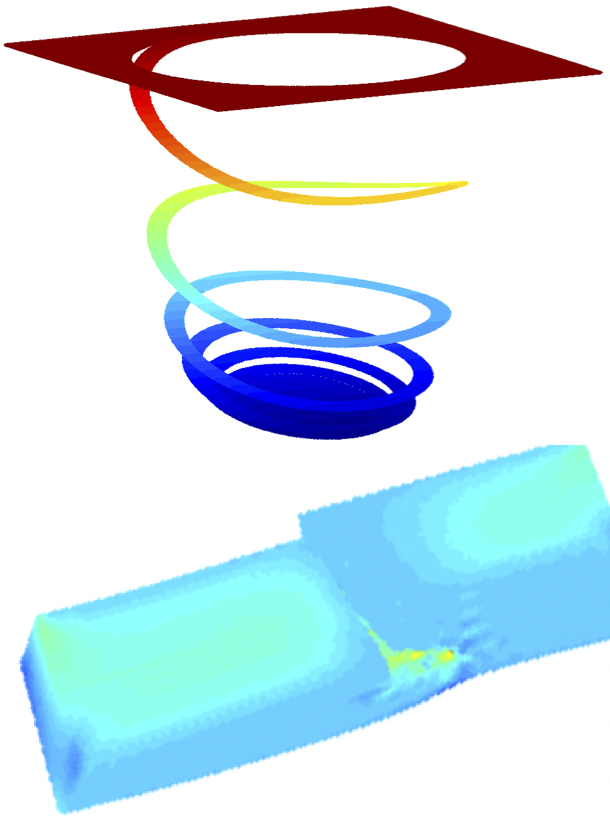
3次元亀裂伝播([13]、Barbieri and Petrinic、2014)およびらせん状割れ目([16]、Sevilla and Barbieri、2014)。
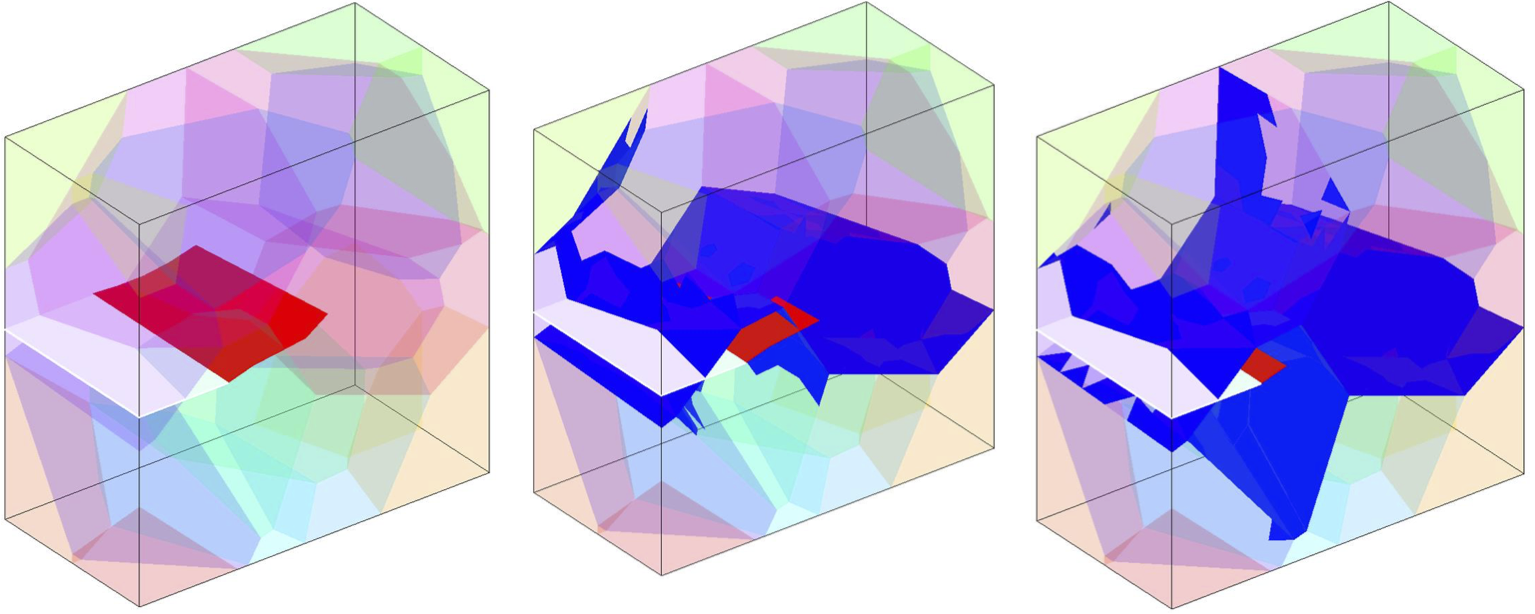
セラミックス微細構造における破壊伝播セラミックス微細構造における破壊伝播。 左から右へ:粒界強度が低下すると粒内(赤色表面)から粒界(青色表面)への移行が起こる(S.Falco、オックスフォード大学の図)。
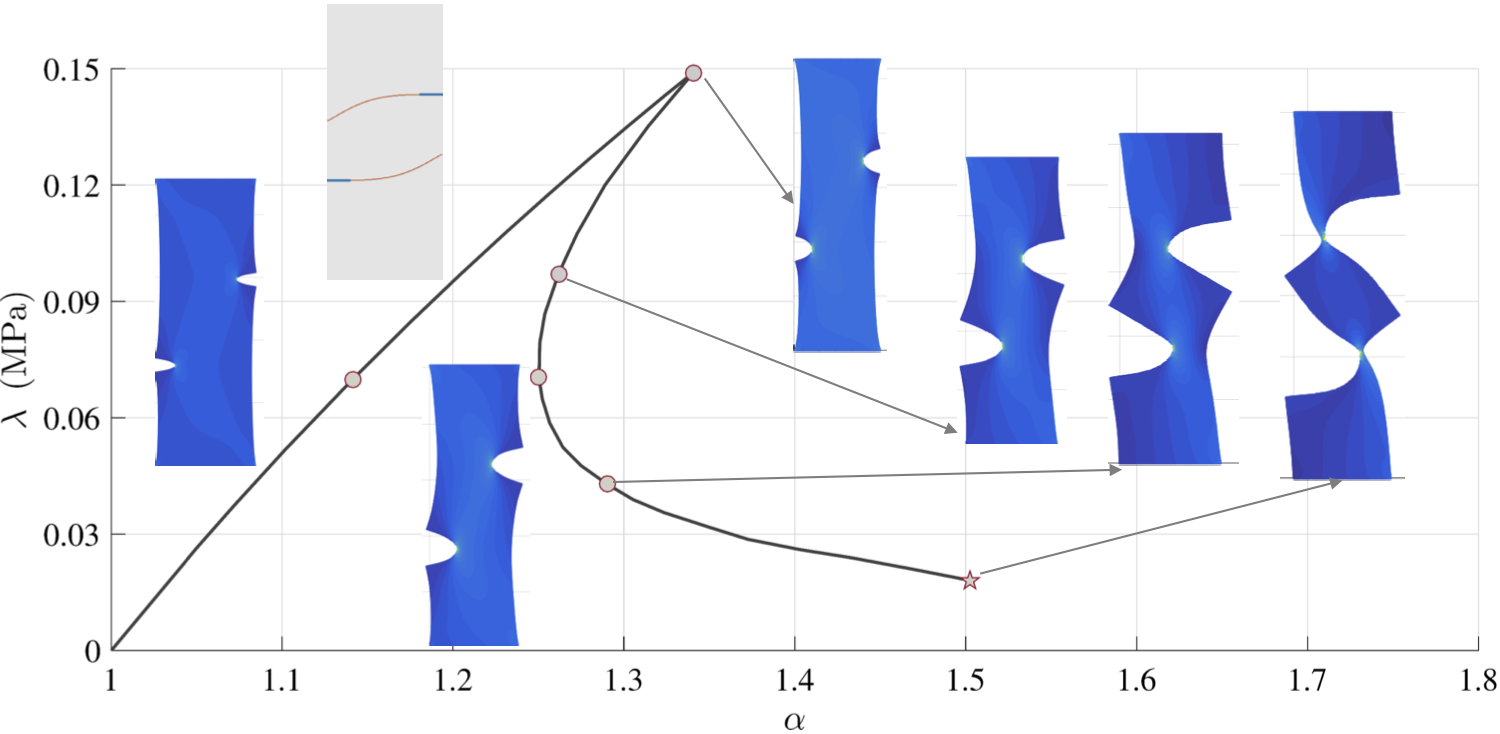
ゴム中の破壊伝播。 一軸牽引λを受ける超弾性体の2つの位置ずれした亀裂の分岐図。 αは伸びを示す。 この曲線は厳しい骨折の典型である([24]、Barbieriら、2016参照)

グラフェン構造の設計 そのアイデアは、あまりにも強く妥協することなく、切れ目を通して非常に変形しやすい構造を得ることです。 このコンセプトは、日本の紙彫刻の芸術に由来します。 きりがみでは、紙のカットのパターンは、ストレッチ時に美しい穴の配置を表示することができます。 伝播するカット、大きな歪み、および材料の非線形の構成的挙動を組み込むことができる非線形ソルバを開発しました。 我々が開発した非線形ソルバは、サイズ効果を捕捉できることに注目することは興味深い。赤いカーブは脆い挙動につながるデザインであり、黒いカーブのものは延性のある破断につながる([24]、Barbieri et al。、2016)。
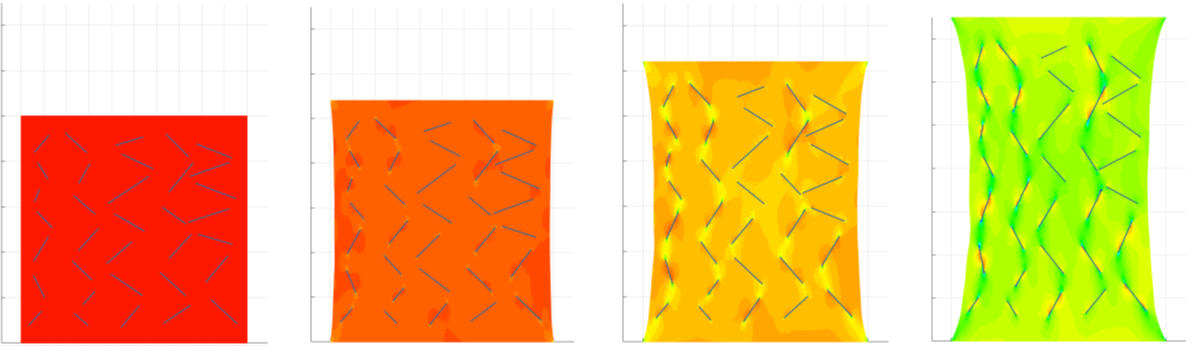
Anticracksは、ゼロ厚硬質介在物のための数学的モデルです。 グラフェンナノプレートレット、または天然のシステムで発生する階層的な微細構造、例えば骨のフィブリルで観察される繊維の再配向のような高度機能材料の強化材のモデリングに役立ちます。 再配向は、ネイチャーが強化して強化するために使用するスマートなメカニズムです。 実際、大きな伸びでは、繊維は荷重の方向に合わせて向きを変え、補強材(抗亀裂)は荷重に耐えて最高の効果を発揮することができます。 左から右に、異なる一軸延伸での変形[18]。
- 非線形固体力学
-
私たちの関心は、単純な線形フックの弾性の法則(弾性物体や材料の歪みは、それに加えられる応力に比例する)で記述できない機械的現象にあります。
例には、ヒステリシス、塑性、大きな変形、大きなひずみ、損傷、接触問題、および折り畳みが含まれます。
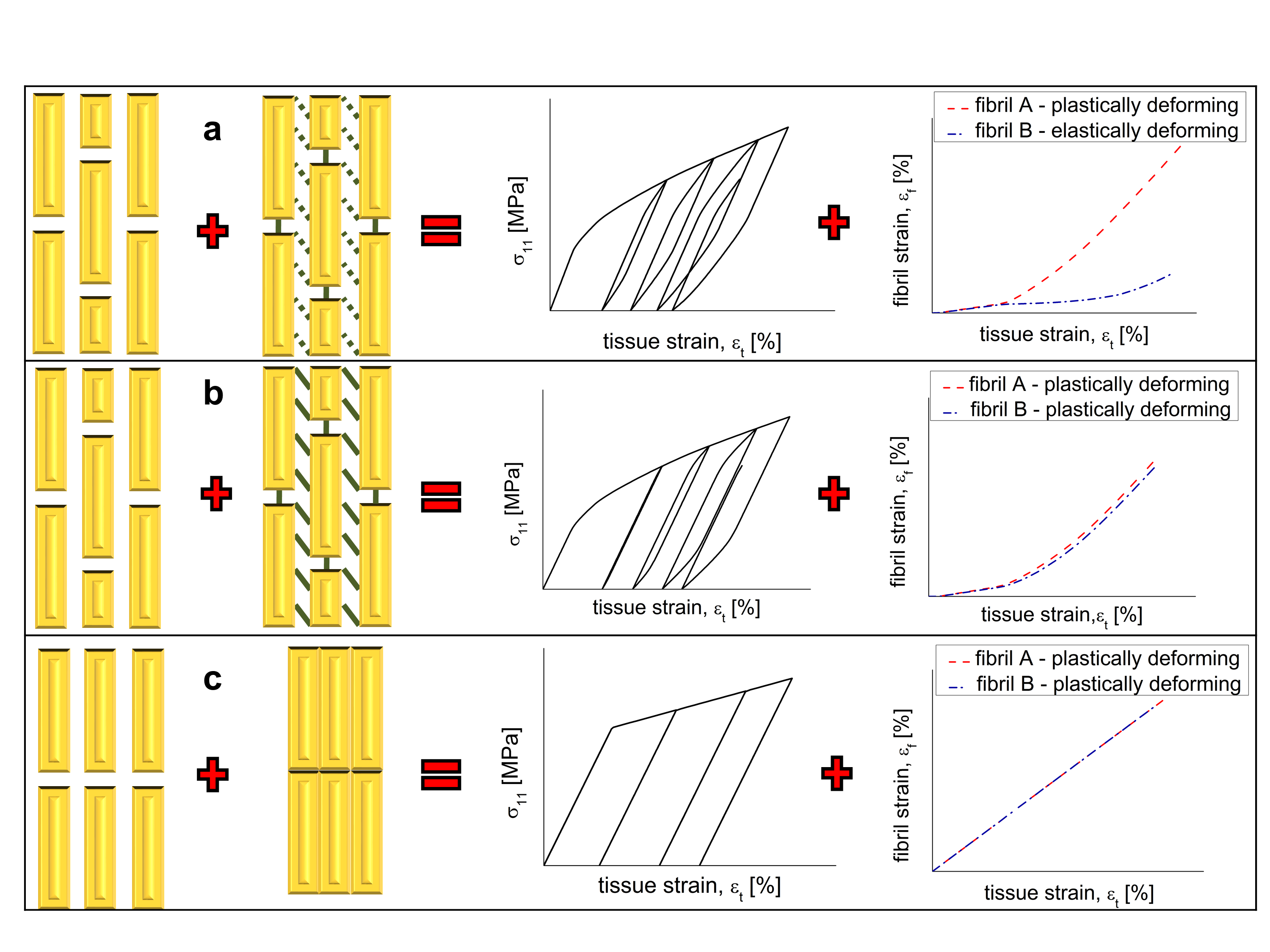
枝角骨の高エネルギー吸収の重要な特徴は、周期的負荷中の大きなヒステリシスであるが、その起源は不明のままである。 鼠径部の引張り荷重下でのその場シンクロトロンX線回折試験 異種線維の変形およびヒステリシスを示した。 枝角骨のナノ構造からのこれらのメカニズムの起源を説明するために、ここで我々は 潜在的複合構造の範囲全体にわたって実験データと予測値を比較する一連の有限要素フィブリルモデルを開発する。 我々は、実験データとの一致を可能にする重要な構造モチーフが、脆弱な鉱化されたコラーゲン原線維の軸方向にずらした配列であり、弱く損傷しやすい線維間界面と結合していることを示している。 P. De Falcoによる図(Max Planckのコロイドと界面の研究所)[25]. この作品は、いくつかのメディア phys.org, FoxNews, EurekAlert!, ScienceDaily.
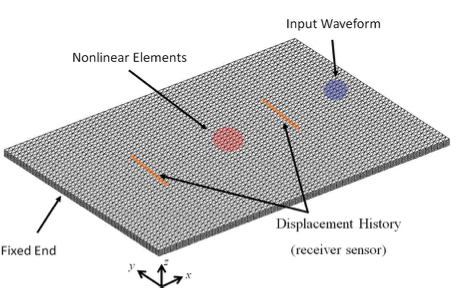
この研究では、非調和と消散の両方のヒステリシス効果を示す微小損傷した材料の連続調波励振下での構造応答の記述を可能にするマルチスケールモデルを定式化するために、準解析Landau式とPreisach-Mayergoyz空間表現を使用しました。 このようにして、偶数および奇数の両方の高調波の生成など、実験的に観測される非線形効果を再現することができる。 このような影響の適用は、損傷した構造の非破壊的評価にあります。例えば、衝撃を受けた構造[11]の損傷の場所を知ることができます。 Figure by F. Ciampa(Bath University)[14]からの図。 作業は、[1]、[5]、[6]、[7]、[11]、[14]、[15]を含むいくつかの論文に出現した。
Publications
Original Publications (Peer-Reviewed)
-
28. “Improving the GJK Algorithm for Faster and More Reliable Distance Queries Between Convex Objects”
M Montanari, N Petrinic, E Barbieri
ACM Transactions on Graphics 36 (3) 2017 -
27. “Towards in situ determination of 3D strain and reorientation in the interpenetrating nanofibre networks of cuticle”
Y Zhang, P De Falco, Y Wang, E Barbieri, O Paris, NJ Terrill, G Falkenberg, NM Pugno, HS Gupta
Nanoscale 9 (31), 11249-11260 2017 -
26. “The in-plane elastic properties of hierarchical composite cellular materials: Synergy of hierarchy, material heterogeneity and cell topologies at different levels”
F Ongaro, E Barbieri, NM Pugno
Mechanics of Materials 103, 135-147 1 2016 -
25. “Staggered Fibrils and Damageable Interfaces Lead Concurrently and Independently to Hysteretic Energy Absorption and Inhomogeneous Strain Fields in Cyclically Loaded Antler Bone”
P De Falco, E Barbieri, N Pugno, HS Gupta
ACS Biomaterials Science & Engineering 2016 -
24. “A J-integral-based arc-length solver for brittle and ductile crack propagation in finite deformation-finite strain hyperelastic solids with an application to graphene kirigami”
E Barbieri, F Ongaro, NM Pugno
Computer Methods in Applied Mechanics and Engineering 2016 -
23. “In situ exfoliation of graphene in epoxy resins: a facile strategy to efficient and large scale graphene nanocomposites”
Y Li, H Zhang, M Crespo, H Porwal, O Picot, G Santagiuliana, Z Huang, E Barbieri, N M Pugno, T Peijs, E Bilotti
ACS applied materials & interfaces 8 (36), 24112-24122 2016 - 22. “Mechanics of filled cellular materials”
F Ongaro, P De Falco, E Barbieri, NM Pugno
Mechanics of Materials 97, 26-47 2016 - 21. “Void ratio based representative volume element for modelling the high strain rate behaviour of granular materials”
F De Cola, A Pellegrino, E Barbieri, D Penumadu, N Petrinic
International Journal of Impact Engineering 91, 46-55 2016 - 20. “A novel consolidation-based representative volume element for granular materials and its application for the characterization of the mechanical response of sand during impact loading”
F De Cola, A Pellegrino, E Barbieri, D Penumadu, N Petrinic
Procedia Structural Integrity 2, 2905–2912 2016 - 19. “New 3D geometrical deposition methods for efficient packing of spheres based on tangency”
F De Cola, S Falco, E Barbieri, N Petrinic
International Journal for Numerical Methods in Engineering 104 (12), 1085-1114 2015 - 18. “A computational model for large deformations of composites with a 2D soft matrix and 1D anticracks”
E Barbieri, NM Pugno
International Journal of Solids and Structures 77, 1-14 2015 - 17. “A new method for the generation of arbitrarily shaped 3D random polycrystalline domains”
S Falco, P Siegkas, E Barbieri, N Petrinic
Computational Mechanics 54 (6), 1447-1460 2014 - 16. “NURBS distance fields for extremely curved cracks”
R Sevilla, E Barbieri
Computational Mechanics 54 (6), 1431-1446 2014 - 15. “Detection and modelling of nonlinear elastic response in damaged composite structures”
F Ciampa, E Onder, E Barbieri, M Meo
Journal of Nondestructive Evaluation 33 (4), 515-521 2014 - 14. “Modelling of multiscale nonlinear interaction of elastic waves with three-dimensional cracks”
F Ciampa, E Barbieri, M Meo
The Journal of the Acoustical Society of America 135 (6), 3209-3220 2014 - 13. “Three-dimensional crack propagation with distance-based discontinuous kernels in meshfree methods”
E Barbieri, N Petrinic
Computational Mechanics 53 (2), 325-342 2014 - 12. “Multiple crack growth and coalescence in meshfree methods with a distance function-based enriched kernel”
E Barbieri, N Petrinic
Key Engineering Materials - Advances in Crack Growth Modeling 170 2013 - 11. “Impact localization in composite structures of arbitrary cross section”
F Ciampa, M Meo, E Barbieri
Structural Health Monitoring 11 (6), 643-655 2012 - 10. “A fast object-oriented Matlab implementation of the Reproducing Kernel Particle Method”
E Barbieri, M Meo
Computational Mechanics 49 (5), 581-602 2012 - 9. “A new weight‐function enrichment in meshless methods for multiple cracks in linear elasticity”
E Barbieri, N Petrinic, M Meo, VL Tagarielli
International Journal for Numerical Methods in Engineering 90 (2), 177–195 2012 - 8. “A meshless cohesive segments method for crack initiation and propagation in composites”
E Barbieri, M Meo
Applied Composite Materials 18 (1), 45-63 2011 - 7. “Time reversal DORT method applied to nonlinear elastic wave scattering”
E Barbieri, M Meo
Wave Motion 47 (7), 452-467 2010 - 6. “Discriminating linear from nonlinear elastic damage using a nonlinear time reversal DORT method”
E Barbieri, M Meo
International Journal of Solids and Structures 47 (20), 2639-2652 2010 - 5. “Detecting loosening/tightening of clamped structures using nonlinear vibration techniques”
F Amerini, E Barbieri, M Meo, U Polimeno
Smart Materials and Structures 19 (8), 085013 2010 - 4. “A meshfree penalty-based approach to delamination in composites”
E Barbieri, M Meo
Composites Science and Technology 69 (13), 2169-2177 2009
- 3. “Evaluation of the integral terms in reproducing kernel methods”
E Barbieri, M Meo
Computer Methods in Applied Mechanics and Engineering 198 (33-36), 2485-2507 2009 - 2. “Waveguides of a Composite Plate by using the Spectral Finite Element Approach”
E Barbieri, A Cammarano, S De Rosa, F Franco
Journal of Vibration and Control 15 (3), 347 2009 - 1. “Nonlinear wave propagation in damaged hysteretic materials using a frequency domain-based PM space formulation”
E Barbieri, M Meo, U Polimeno
International Journal of Solids and Structures 46 (1), 165-180 2009
Books and Book Chapters
- 1. “Computational techniques for simulation of damage and failure on composites”
J Curiel Sosa, R Brighenti, M C Serna Moreno, E Barbieri (2015).
In Structural Integrity and Durability of Advanced Composites, Woodhead Publishing, edited by P. Beaumont, C. Soutis, A. Hodzic.
