スマホを落とした時に画面がバキバキに割れてヘコんだことはありませんか? そもそも、なぜスマホの画面はあんな割れ方をするのでしょうか? じつはこのような物理現象のシミュレーションに世界で初めて成功したのが海洋研究開発機構(JAMSTEC)数理科学・先端技術研究開発センター(MAT)の廣部紗也子研究員です。なぜこの現象の予測が難しいのか?そもそもガラスが割れるとはどんな現象なのか? 基礎から世界初のシミュレーション手法、その応用についてお話を伺いました。(取材・文:岡田仁志)

スマホのガラスは内部に力が残っている
──今回、廣部さんが破壊過程のシミュレーション(再現)に成功された化学強化ガラスは、身近なところではスマートフォンのディスプレイに使われていますよね。「強化ガラス」というわりに、落としたときに凄まじい割れ方をするのが不思議です。
たしかに、ちょっとだけ浅いヒビが入るだけで済むこともあれば、蜘蛛の巣みたいにグチャグチャに割れることもありますよね。ふつうのガラスとは、ずいぶん割れ方が違います。これは、化学強化ガラスに「残留応力」があるからなんです。
──残留応力? それは何でしょうか。
まず、応力というのは物体に生じる力のことです。ガラスでも金属でも、物が変形したり破壊したりするときには、外から何らかの力がかかっていますよね? その荷重に応じた力が、物体の内部に発生します。残留応力は、なんらかの理由で応力が内部に残留している状態です。
──いま私が手にしているスマホのディスプレイにも、応力が残っているんですか? そんなふうには見えませんけど…。
見た目にはわかりませんが、そのガラスの表面には「圧縮」の応力、そしてガラスの内部には「引張(ひっぱり)」の応力が残っているんです。圧縮の残留応力と引張の残留応力がつり合っているので、それ以上変形はしません。
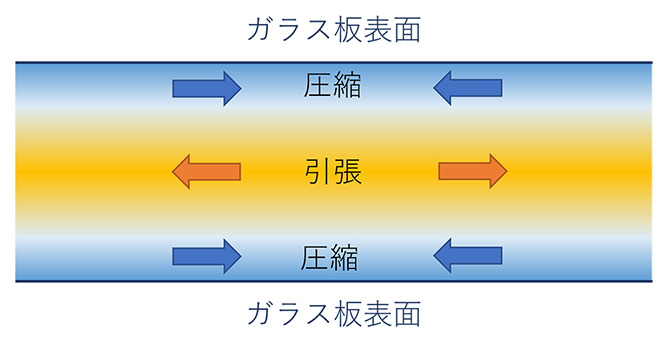
──ガラスの表面と内部で綱引きをしてるような感じなんですね。そんなスリリングな状態だとは思っていませんでした(笑)。
強化ガラスはどのように造られるのか
強化ガラスの残留応力については、17世紀から知られていた「プリンス・ルパートの滴」(「オランダの涙」とも呼ばれます)が有名です。ネットで検索するとおもしろい動画が出てきますよ。
溶けたガラスを冷水に落とすと滴形に固まるんですが、その頭の部分は、ハンマーで思い切り叩いても割れません。ところが、細く延びた尻尾の部分を折ると全体が爆発するように破砕します。

これは、冷えて固まる過程で、外側が内側よりも先に急激に冷え固まって収縮するので、表面には圧縮応力、それと釣り合うように内側には引張応力が残留しているのです。
「プリンス・ルパートの滴」は熱強化ガラスと呼ばれるものと同じ原理ですが、スマホのディスプレイなどの化学強化ガラスは、ふつうのガラスに含まれているナトリウムイオンをカリウムイオンに置換しています。ガラスを硝酸カリウム溶融塩に浸しておくと、ナトリウムイオンが出て行って、空いたところにカリウムイオンが入ってくるんです。
すると、ナトリウムイオンよりカリウムイオンのほうが大きいので、ガラスの表面がミチミチに押し合いへし合いしている状態になります。それによって、圧縮するような応力が発生する。だから、表面に小さな亀裂が入っても、押されて閉じるんですよ。
──なるほど、圧縮応力があるからヒビが広がりにくいんですね。
ですから表面の傷に対しては、たしかに「強化」されているんです。ふつうのガラスの場合、ちょっとした亀裂があると、次に何か衝撃が加わると簡単に割れてしまいますよね。でも強化ガラスの表面に入った亀裂は、それ以上はなかなか進みません。
ただし強化ガラスの内部には、表面の圧縮応力とつり合う引張応力が残留しています。そのため、傷が深いところまで侵入すると、引張応力のせいで亀裂がどんどん開いて進んでいき粉々に割れてしまうんです。
残留応力にはそういうリスクがあるので、物づくりでは基本的に嫌われます。たとえば金属製品を加工するときに行われる「焼なまし」(材料を適当な温度に加熱してから徐冷する熱処理)も、残留応力を取り除くのがひとつの目的です。
──ふつうは嫌われる残留応力を逆手に取ったのが、強化ガラスということなんですね。
これが実験とシミュレーションの結果!
――この図の右側が廣部さんのシミュレーションで、左側が化学強化ガラスを実際に割ったときの実験結果ですね。この再現性の高さに驚きました! でも、そもそもなぜ「残留応力」のある強化ガラスはシミュレーションができなかったのでしょうか。
はい。まず、残留応力のないプレーンなガラスは材質が均質かつ等方的だし、ほとんど変形しないで割れるので、「破壊力学」という研究分野では、理想的な材料として以前からいろいろな実験やシミュレーションの対象として使われていました。変形が少なく、亀裂が進む向きに材質が影響を与えないので、解析の条件が比較的シンプルになるんですね。
でも残留応力があるだけで条件が一気に複雑になるので、数値解析が非常に難しい。シミュレーションができないので、ガラスメーカーは実際につくったものを破壊する実験をくり返して、その割れ方を調べるしかありませんでした。
──では、複雑になる残留応力の破壊解析についてのお話は後回しにして、簡単なほうからうかがったほうがいいかもしれませんね(笑)。破壊力学では、そもそもガラスが割れる現象をどのように考えているのでしょう。
そもそもモノが割れるってどんな物理現象?
まず、物体の割れ方は材料の種類によって違います。大きく分けると、ガラスに代表される脆性(ぜいせい)材料と、金属のような延性(えんせい)材料の2種類がありまして……。
──「脆性」と「延性」ですか。文字を見ないと何のことかわからないですね(笑)。
はい、この分野はなぜか難しい言葉が多いんですよ(笑)。ガラスは力をかけると、グニャリと変形することはほとんどなくて、あるところでパリッと割れますよね。そういう割れ方を「脆性破壊」といいます。一方、金属は力をかけるとグニューンと曲がりますし、引っ張ると延びます。たとえば針金なんか、重いっ切り曲げてもなかなかちぎれませんよね。こちらは「延性破壊」といいます。
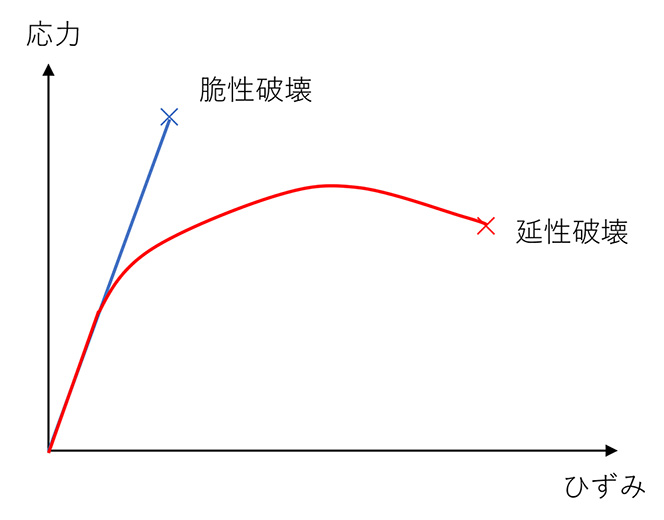
その脆性破壊と延性破壊の違いを表したのが、「応力−ひずみ曲線」という図です。縦軸は物体にかけた力、横軸は物体のひずみ具合。要は物体が伸びた量だと思ってください。この図では、どちらも×印のところで破壊が生じているのですが、脆性破壊のほうは、応力が大きくなってもひずみ具合が小さいですよね。それに対して、延性破壊のほうは同程度の応力でもひずみ具合がどんどん大きくなっています。
──このグラフには時間軸がありませんが、力をかけた時間は関係ないんですか?
はい、応力とひずみの関係だけです。たとえば中学で習う「フックの法則」も時間は無関係ですよね。フックの法則は、バネの伸びる長さとバネに加わる力の大きさの関係を表しています。式はF=kxで、Fは力、kはバネ定数、xはバネが伸びた長さなので、どれぐらいの力をかけるとどれぐらいバネが伸びるかは、時間と関係なく決まっているわけです。脆性破壊や延性破壊もそれと同じで、時間は関係ありません。
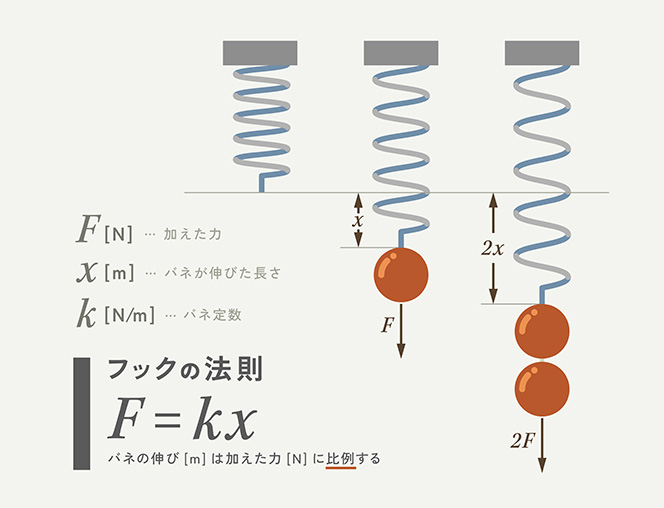
ただ、フックの法則では先ほどの式のとおり力とバネの伸びた長さが比例し続けますが、実際のバネはずっと引っ張り続けると、あるところからバネが伸びきって戻らなくなりますよね。
このように、力をかけなくても物体が元の形に戻らなくなることを「塑性(そせい)変形」といいます。また難しい言葉ですが(笑)。
バネに塑性変形が起きると、もうフックの法則は成り立ちません。フックの法則が成り立たない状態になってから破壊するのが延性材料、フックの法則が成り立っている間に破壊するのがガラスのような脆性材料というわけです。
ガラスの脆性破壊のメカニズムとは?
基本的には、材料内部にある微小な欠陥や亀裂が、外から力が加わることによって拡大していくことで脆性破壊は起こります。
たとえどんな小さな亀裂であっても、亀裂の先端では「応力集中」と呼ばれる現象が起こって、実際にかけている力よりはるかに大きな力が発生してしまいます。そのせいで亀裂が急速に拡大していくんですね。そしてこの亀裂が材料全体を貫通すると、材料は一気に破損して、脆性破壊が起こるというわけです。
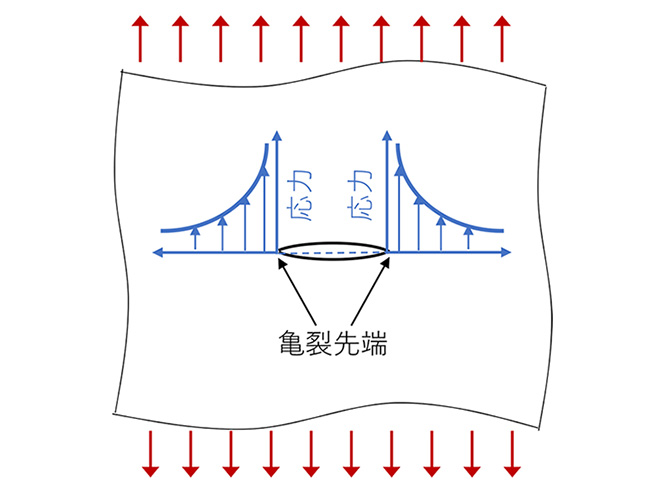
──ガラスの割れ方はいろいろだと思います。それがシミュレーションによって再現できるのでしょうか?
たしかに、ガラスはいろいろな割れ方をしますよね。何か硬い物が衝突して割れることもあれば、熱したガラスのコップに冷たい水を注いだときに温度差で割れることもあり、それぞれ違った割れ方をします。
シミュレーションを行うときは、破壊の要因となる衝突した物体の重さや速度、あるいはそこで生じた温度変化などの数値データも取り入れて計算します。破壊の要因となるそれぞれの現象と破壊現象の両方をモデル化し、それらのモデルを使って数値計算をすると、どんな割れ方になるのかがシミュレーションできるんです。
強化ガラスのシミュレーションができなかった理由
──でも化学強化ガラスのように残留応力がある場合は難しいんですね?
そうなんです。そもそも破壊という現象は、物体が変形することで溜まったエネルギーを解放する過程なんですね。破壊が始まるとエネルギーが解放されて、あるところまで解放されたら終わる。シミュレーションは、その過程を定量的に評価しなければなりません。
ふつうの残留応力のないガラスでは、破壊するためにエネルギーを流入させる、つまり外から力をかける必要があります。外からエネルギーが流入している間は、そのエネルギーを解放することで破壊が続くのですが、エネルギーの流入を止めてしまえば、破壊は止まる。この過程は比較的理解しやすいんです。
ところが残留応力のあるガラスは、外から力を加えていないのに、内部に変形のエネルギーが溜まっている状態にあります。そのため一度亀裂が入ると、外から力を加えていなくてもどんどん勝手に破壊が進んで、もともと内部に溜まっていたエネルギーを解放していってしまいます。
しかも、その亀裂によって材料は分割されたり形が変わったりしていますよね。そこにもまだ残留応力があるので、それぞれの場で新たに「圧縮」と「引張」がつり合う状態に向かおうとするんです。
──亀裂が進むにつれて、その場その場で「綱引き」のバランスが変わっていくんですね?
そういうことです。亀裂が進むごとにエネルギーの解放と再分配が起きるんです。そして、亀裂が進む速度は毎秒2000メートル近くにもなります。ですからシミュレーションのためには、エネルギーが解放される過程と新しい状態に再分配される過程を同時に解いていかなければなりません。しかも、これらの過程が外から何もしていないのに勝手にかつ高速に進んでいく。そこがいちばん難しいところです。
ふつうのガラスは、外から力をかけて割れたら、もう力は伝わりません。そこでおしまいです。でも化学強化ガラスはいたるところに応力が溜まっているので、そこでおしまいとならず、それらの溜まっていた応力がどうなっていくかをいちいち計算に入れていく必要があるんですよ。

──そのための新しい計算方法を開発したのですか?
使ったのはPDS-FEM(粒子離散化有限要素法)という破壊シミュレーションのための手法です。その基本的なものは、20年ほど前に提案されていました。でも、そのままでは残留応力がある場合の破壊の計算はできません。それを定式化する過程で、残留応力を含む形に変えることで、化学強化ガラスの破壊をシミュレーションできるようにしました。
ガラスの破壊の数理モデルをつくるには
──具体的には、何をどうやって計算するのでしょうか。
もともとFEM(有限要素法)は物体の変形を解析するのによく使われるメジャーな手法です。解析の対象となる場を細かいグリッド(格子)に分割して、個別に計算するんですね。
でもFEMは連続的な変化を解析するものなので、不連続な変化を起こす破壊現象を解くことはできません。それを破壊解析に使えるよう改良したのがPDS-FEMです。
3次元だと話がややこしくなるので2次元で説明しますが、FEMでは三角形のメッシュで場を分割します。PDS-FEMでは、図のように、その三角形のメッシュ(ドロネー分割)から自動的に決まる「ボロノイ分割」を使って、さらに違うグリッドをつくるんですね。三角形の重心と各辺の中点を結ぶ線を描くと、図のようなゴロッとした図形ができる。これがボロノイ分割です。
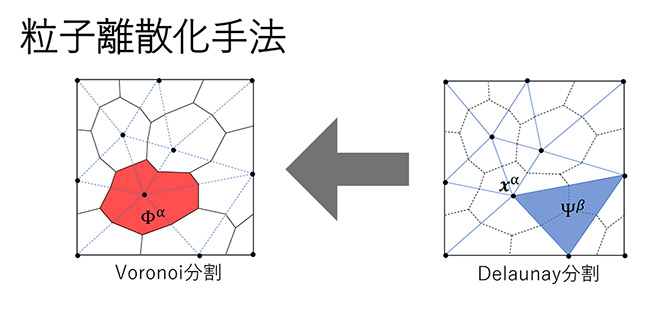
── 一見するとランダムな形ですが、なるほど、そういうルールに基づいているんですね。もとの三角形も形やサイズがまちまちですが、それはどうやって決めるんでしょう。メッシュというと、方眼紙みたいに同じ形のグリッドで均等に分割するイメージがありますが。
同じ形で均等に区切ったほうが計算は楽になるのですが、一般的にランダムな形の三角形を使う方が複雑な形状のモデルでも柔軟に対応できメッシュ分割しやすいというメリットがあります。また、PDS-FEMでは亀裂がボロノイ分割の境界上で再現されます。その場合、同じ形で均等に区切っていると、ボロノイ分割の境界に特定の方向性が見えてしまい複雑な亀裂の形状を再現しにくくなるんですね。
こういった理由から、わざと形も向きもバラバラになるように分割することを「ランダムメッシュ」もしくは「非構造メッシュ」といいます。 ただ、ランダムといっても、三角形の大きさがあまりにも違いすぎたり、極端に尖った三角形があると計算上の問題が生じるので、面積や点と点の距離や三角形の形(アスペクト比)などがある範囲に収まるようにはしなければいけません。そのさじ加減も難しいので、いい感じに分割する「メッシュ・ジェネレーター」の開発を専門的に手がける研究分野もあるくらいです。
実際の実験はどのように行ったのか?
──そうやってつくったグリッドの大きさはどれぐらいですか?
私のやったシミュレーションでは、三角形の一辺の長さが10マイクロメートル程度ですね。実際の実験では厚さ0.7ミリメートルのガラスの板を使用していますので、これを70等分するくらいの細かさです。
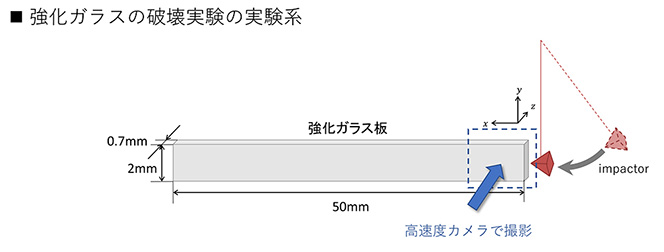
シミュレーションでのメッシュのサイズは、試行錯誤が必要ですね。粗いと現象の細かな変化を捉えきれないので、「この粗さで十分かどうか」を検証しなければいけません。徐々に細かくしていって、それ以上に細かく分割しても結果が変わらなくなれば、そこで計算が収束したことになります。
世界初!残留応力場内での破壊の数理モデルは
──ボロノイ分割のやり方はわかりましたが、それにはどんな意味があるのですか?
三角形のメッシュに加えて、このような分割も用いることで、破壊によって生じる不連続な面を表現できるようにしています。三角形メッシュの中では、変位も応力も連続的になっているので、三角形メッシュだけでは亀裂が生じたときに不連続になるという変化をどう定義すればいいかわかりません。だから一般的なFEMでは破壊シミュレーションができないんですね。
それに対してPDS-FEMでは、ボロノイ分割で定義されたグリッドを「ボロノイ粒子」と呼んで、その中では変形が起きないものと見なします。それ自体は変形も破壊もない剛体だとすると、亀裂ができるのはボロノイ粒子の境界面だけですよね。
このボロノイ粒子同士は剛性マトリクスと呼ばれるバネのようなものでつながっていると見ることができて、そのつながりを切ることで破壊という現象を表現するのが、PDS-FEMという手法のイメージです。このモデルをベースにして、残留応力によってボロノイ粒子にどんな力がかかるのかと、残留応力によって生じる変形のエネルギーが亀裂が進むことでどれぐらい解放されるのかを、定量的に計算できるようにしました。
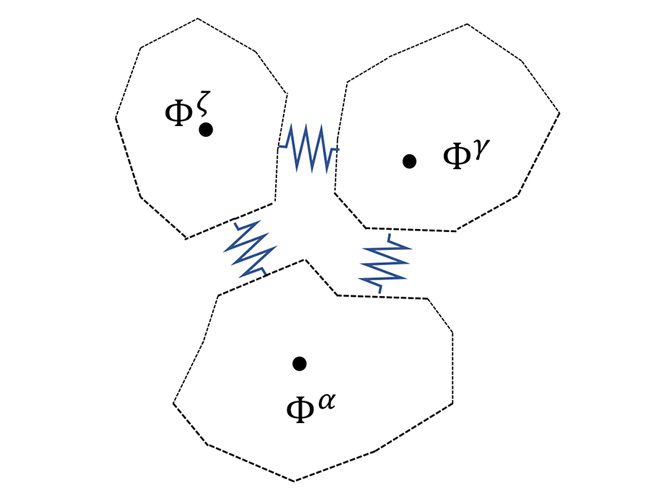
もちろん、ボロノイ粒子は計算のために定義したものですから、現実の材料で起きる現象と完全には一致しません。そこには、離散化(連続的な現象を細かい領域に分割して計算すること)の限界があります。これはFEM全般に言えることですね。
確かに、三角形のグリッドやボロノイ粒子のサイズを小さくすればするほど、シミュレーションの結果はより現実に近づいていきます。でも、一方で、細かなメッシュにすればするほど計算量がものすごい勢いで増えていってしまいます。計算ができる範囲で、自然現象に近いギリギリのところまで迫れる境目を追いかけるような感じですね。
シミュレーションと実験結果を比較すると
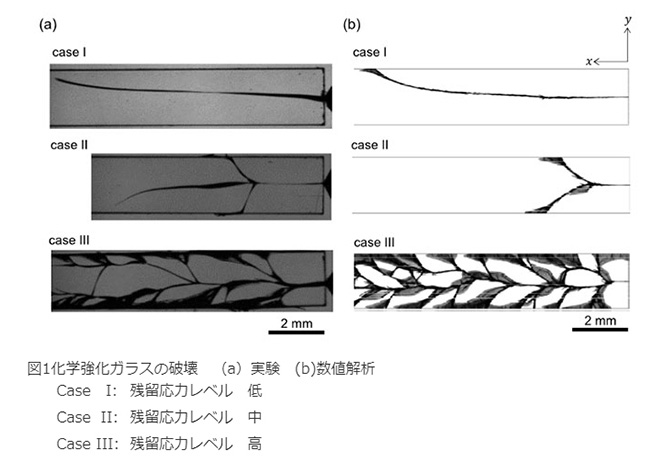
──なるほど。その「自然現象」が破壊実験で得られた図a(左)で、そこに肉迫したシミュレーションの結果が図b(右)ですよね。

化学強化ガラスの破壊過程 実験とシミュレーションの比較(動画:JAMSTEC)
実験でもいつも同じ割れ方をするわけではないので、何をもって「シミュレーションと同じ」と見なすかはなかなか難しいのですが、残留応力レベルの低い「caseI」はかなり高い精度で再現できました。実験でも、この残留応力レベルでは必ず亀裂が1本だったんです。
亀裂の方向も同じになっていますが、これはたまたまですね。実験では亀裂が下に向かうこともありましたし、シミュレーションでもメッシュを変えると下向きになりました。でも数値解析としては、亀裂の本数が再現できたことが重要です。
──残留応力レベルが中程度の「caseII」では、実験で生じた3本の枝分かれが、シミュレーションでは2本ですね。
どちらも枝分かれが1回だけ起きているという意味では、それなりに再現できたと評価しています。でも実験では必ず3本に分かれたので、これは今後の課題が得られました。最初の衝撃を与えるところが実験とシミュレーションでは異なるので、もしかしたらそこを改善すべきなのかもしれません。
というのも、実験では強化ガラスの端におもりをコツンと当てて破壊するんですね。でもその衝突も含めて解析するのは大変なので、シミュレーションでは引張応力の領域に初期亀裂を入力しました。
残留応力の高い「caseIII」も、定性的にはかなり再現できたと思いますが、まだ研究の余地はあると思います。残留応力が高いほど亀裂の形状も複雑になりますから。
残留応力場の破壊シミュレーションを応用すれば!
──こうしたシミュレーションが可能になると、強化ガラスのつくり方も変わるのでしょうね。
これまでは、何度も何度も人海戦術で実験しなければ、破壊のプロセスがわかりませんでした。でもこうしたシミュレーションによって、残留応力レベルをどう設定すればどんな割れ方になるのかを、実験コストをかけずに理論的に予測できるようになります。
たとえば自動車のウインドウには熱強化ガラスが使われているのですが、割れたときに危なくないよう、丸い破片にしたいそうです。どうすれば破片が丸くなるかを実験で試行錯誤するのはものすごく大変ですよね。このシミュレーションを応用して、希望の形に割れるガラスの開発にも活用できるのではないかと考えています。

この残留応力場のシミュレーションは、さらに地震断層での破壊の起こり方や北極や南極の氷の割れ方など、さまざまなことに応用ができるのではないかと考えられています。その応用と今後の研究について、次の記事「世界は数式で表されるのか?「残留応力場」の破壊シミュレーションから地震断層や北極の氷の破壊予測に挑む!」で詳しく紹介します。
取材・文:岡田仁志
図版作成:酒井春
撮影:松井雄希(講談社写真部)
取材協力・図版提供:数理科学・先端技術研究開発センター 廣部 紗也子 研究員